Question

The equivalent capacitance in between points A and B in the following combination is $5x\mu F$. Find the value of $x$.

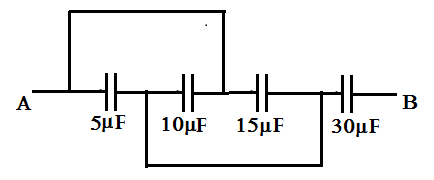
Answer 1

Hint: The given circuit is the combination of the capacitors. Here the circuit is looking like a simple circuit but it contains some of the capacitors in parallel and the some in the series. To get the clear idea we should prepare an equivalent circuit for the above circuit diagram.

Complete step by step answer:
So, the equivalent circuit for the given circuit in the problem is as follows,

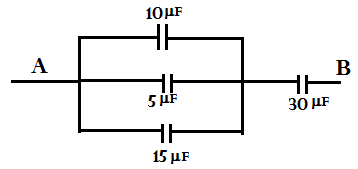
Now on seeing the above equivalent circuit we see that the three capacitors are in parallel and one capacitor is in the series combination of the equivalent of the parallel combination.
So now we will proceed step by step assuming two parts of the circuit, one is parallel combination part and the other one is the series combination part,
So, for the parallel combination part,
The equivalent capacitance will be calculated as fellows,
Let the equivalent capacitance of the parallel combination = \[{C_P}\]
We know that the equivalent capacitance of a parallel combination set of the capacitors is the total sum of the individual capacitance.
So, \[{C_P}\]=$10 + 5 + 15 = 30\mu F$
Now this equivalent capacitance will be in series combination with the remaining one capacitor of magnitude $30\mu F$.
So, the circuit will look like this,
 

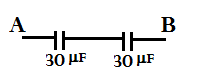
So now the equivalent capacitance of the resultant circuit in between the point A and B is,
${C_{AB}} = \dfrac{{30{C_P}}}{{30 + {C_P}}}$
$ \Rightarrow {C_{AB}} = \dfrac{{30 \times 30}}{{30 + 30}} = \dfrac{{900}}{{60}}$
$ \Rightarrow {C_{AB}} = 15\mu F$
Now in the question it is given that the equivalent capacitance in between points A and B in the following combination is \[5x\]$\mu F$.
So ${C_{AB}} = 5x$
$ \Rightarrow 15 = 5x$
$ \Rightarrow 5x = 15$
$ \Rightarrow x = \dfrac{{15}}{5} = 3$
$ \Rightarrow x = 3$

Hence the value of $x$ is $3$.

Note: Here we see the combination of the capacitors. The capacitor is an electrical device which is used to store the electrical energy. They are composed of the two plates which are separately positively charged and negatively charged. This keeps stored energy and when we need a sudden increase in the amount of the energy then this energy is being used by the circuit. These capacitors are also known as condensers.