Question

What will be the equivalent resistance between point A and D?

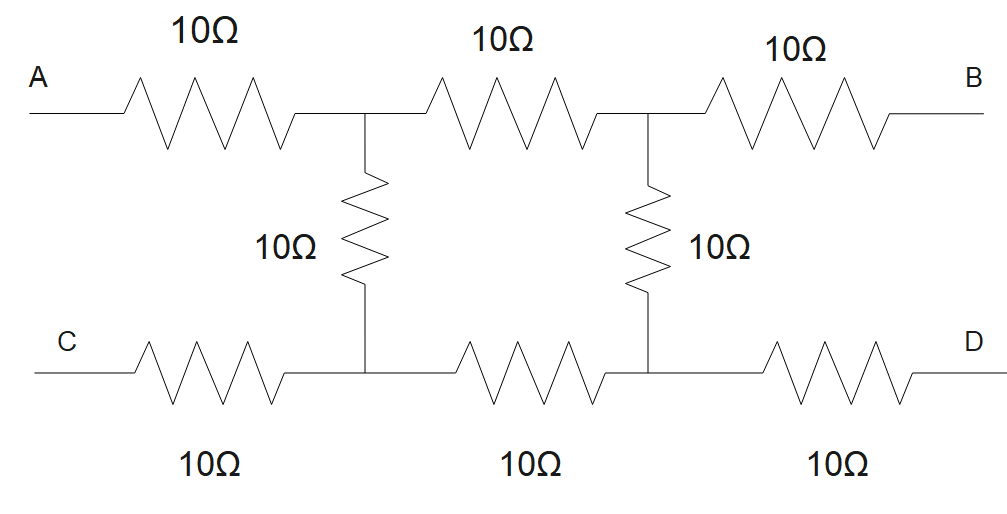
A.) 10Ω
B.) 20Ω
C.) 30Ω
D.) 40Ω

Answer 1

Hint:To find the equivalent resistance between two points the first step we need to do is to find the shortest past by which current can travel and then we need to find out what resistance is out of circuit in that path. We know that current always take the shortest path so it is very important to first know what path our current is taking.

Complete answer:
In the above question, the circuit seems very complex at first sight. So the first thing we need to do is reduce the circuit to a simpler form. When the current starts from point A it will take one of the two paths either it will travel from point A to D via APQSD or from path APRSD, because no other path is possible to complete the circuit. In both the paths the resistance connected near the point C and point B will be useless because no current will be supplied to them and hence, we will not take them into consideration.
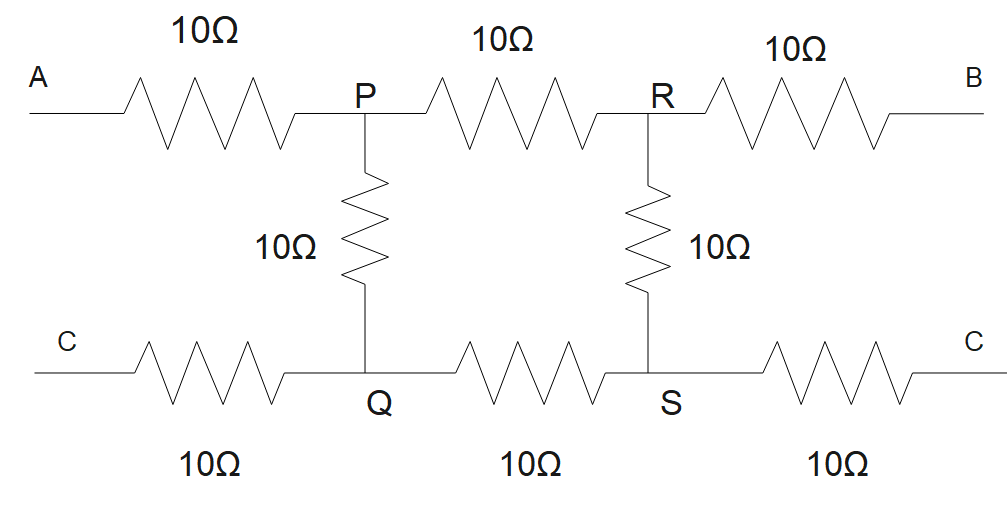
The below figure shows all the points with the path specified above.

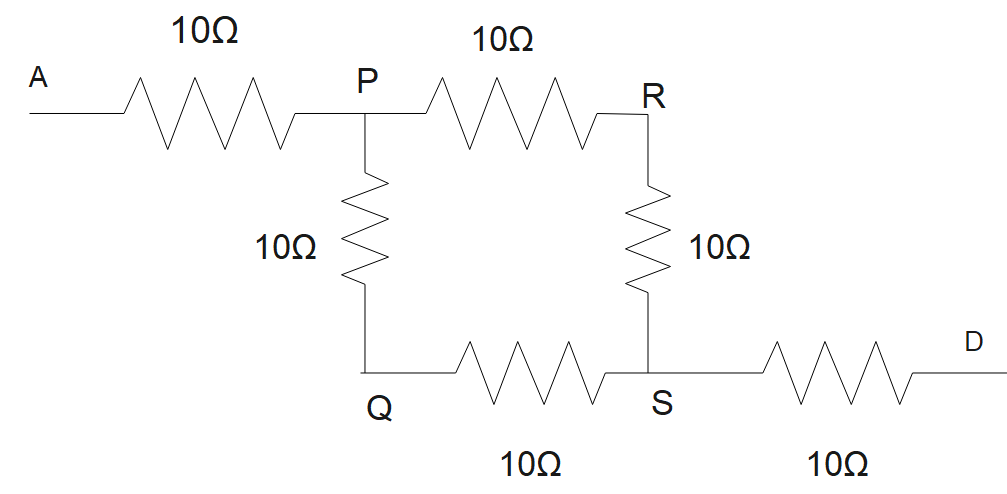
Now we need to make another diagram that will be the equivalent diagram for the above one.

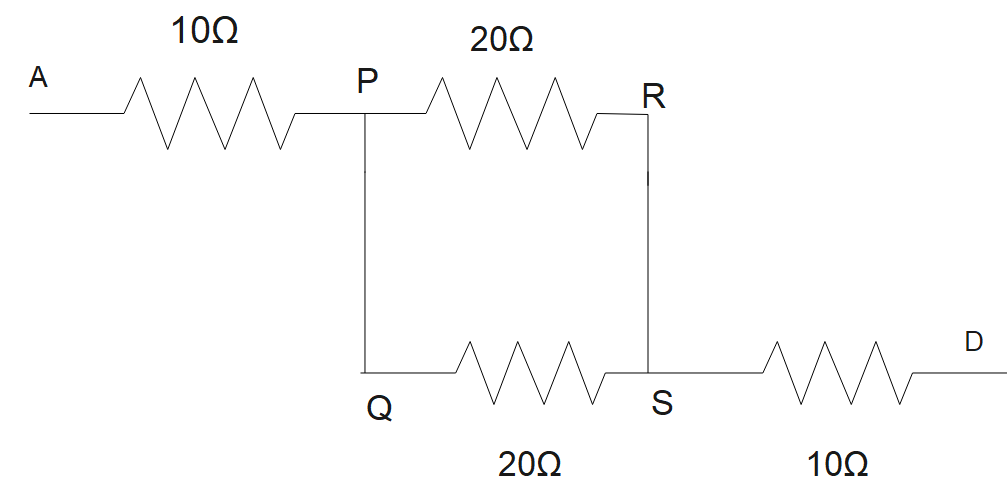
Now in the above figure we can see that the resistance between point P and S via R and Q are in series.
We know that to find equivalent resistance in series we have to simply add both the resistance
So \[{{R}_{eq(PQS)}}=20\Omega \]
And \[{{R}_{eq(PRS)}}=20\Omega \]
Now the figure becomes,

Now both the $20\Omega $ resistance are in parallel connection with each other, so we know that the equivalent resistance for parallel connection is by
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
So ${{R}_{eq}}=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
Now putting the values, we get,
${{R}_{eq}}=\dfrac{20\times 20}{20+20}$
${{R}_{eq}}=10\Omega $
Now all the resistance between the points A to D becomes in series,
Hence, we can add all of them and get the final equivalent resistance.
$R=10+10+10$
$R=30\Omega $

Hence, we can conclude that option (C) $R=30\Omega $ is the correct answer.

Note:
When a question about finding the equivalent resistance is given, always redraw the diagram in a simpler form and try to reduce as much resistance as possible. Keep everything to minimum so that the circuit will be small and not a complex one. After making an equivalent circuit find the circuits with series and parallel connection and then solve the question by finding the equivalent resistance between them.