Question

The exterior angle value is \[110^\circ \] and any one of the interior opposite angle values is \[30^\circ \], then find the value of the remaining angles of the triangle.

Answer 1

Hint:
Here we will first find the value of another interior angle by using the concept of the exterior angle property of the triangle. Then by using the sum of the angles of the triangle, we will find out the value of the third angle of the triangle.

Complete step by step solution:
It is given that the exterior angle of a triangle is \[110^\circ \] and one of the interior opposite angles is \[30^\circ \].
So we will draw the diagram of the triangle using the given information.

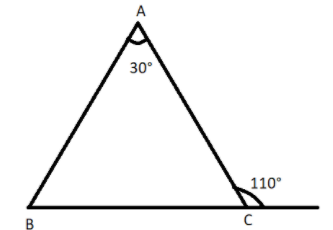
Then by using the concept of the exterior angle property of the triangle, we get
 \[\angle A + \angle B = 110^\circ \]
It is given that the angle A is \[30^\circ \]. Then by putting the value of A in the above equation, we get
 \[ \Rightarrow 30^\circ + \angle B = 110^\circ \]
Subtracting \[30^\circ \] from both sides, we get
 \[ \Rightarrow \angle B = 110^\circ - 30^\circ \]
 \[ \Rightarrow \angle B = 80^\circ \]
We know that the sum of all the angles of a triangle is equal to \[180^\circ \]. Therefore, we get
 \[\angle A + \angle B + \angle C = 180^\circ \]
By putting the value of angle A and angle B, we get
 \[ \Rightarrow 30^\circ + 80^\circ + \angle C = 180^\circ \]
Adding the terms, we get
 \[ \Rightarrow 110^\circ + \angle C = 180^\circ \]
Subtracting the terms, we get
 \[ \Rightarrow \angle C = 180^\circ - 110^\circ \]
 \[ \Rightarrow \angle C = 70^\circ \]

Hence, the value of the remaining angles of the triangle is \[80^\circ \] and \[70^\circ \].

Note:
Here we need to keep in mind the exterior angle property of the triangle. It states that an exterior angle of a triangle is always equal to the sum of the two opposite interior angles of the triangle. Vertically Opposite Angles (vertical angles) are the angles opposite each other when two lines intersect or cross each other and pairs of vertically opposite angles (vertical angles) are always equal to each other. We should know that the corresponding angles are the angles which are formed at the corresponding corners when the transversal line is passed through the two parallel lines.