Question

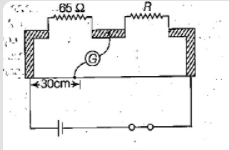
The figure shows a meter bridge with null deflection in the galvanometer. The value of unknown resistance R is?

A. \[158\Omega \]
B. \[151.61\Omega \]
C. \[128.65\Omega \]
D. \[130\Omega \]

Answer 1

Hint: We need to know the concept of Meter Bridge.
We need to know the conditions to attain balance of the meter bridge.

Complete step by step answer:
Resistance is a measure of opposition to current flow in an electrical circuit.
The galvanometer is the current measuring instrument which is mostly used in derides and potentiometers for showing the zero current.
A meter bridge also called a slide wire bridge is an instrument that works on the principle of a Wheatstone bridge. A meter bridge is used in finding the unknown resistance of a conductor as that of in a Wheatstone bridge.
The bridge is said to be balanced when no current flows through the galvanometer. When there is no current flowing through the bridge the potential difference or voltage between the points D and B is zero.

From balancing condition of Wheatstone Ledge
$\dfrac{P}{Q} = \dfrac{R}{S} \Rightarrow \dfrac{P}{R} = \dfrac{Q}{S}.....(1)$
Here $P = 65\Omega $
$
 R = R = ? \\
  {L_1} = 30cm \\
  {L_2} = 100 - 30 = 70cm \\
  R = \dfrac{{\rho l}}{A} \\
$
$\rho $ is the density of the wire, l is the length of the wire, A is the area of the cross section of wire and R is the resistance of the wire.
In the Meter Bridge the wire is of uniform cross section.
So,
$
  R\alpha L \\
  \therefore \dfrac{Q}{S} = \dfrac{{{L_1}}}{{{L_2}}} \\
$
From Equation (1)
$
  \dfrac{{65}}{R} = \dfrac{{{L_1}}}{{{L_2}}} = \dfrac{{30}}{{70}} = \dfrac{3}{7} \\
  \therefore R = \dfrac{{65 \times 7}}{3} \\
   = \dfrac{{455}}{3} = 151.67 \\
$

So, the correct answer is “Option B”.

Note:
We have to change all units in the SI system. Or at least the same quantities should have the same units.
We know that the Resistance is directly proportional to the length and indirectly proportional to the area. $R\propto \dfrac{L}{A}$.