Question

The foci of an ellipse are S(-1,-1), S’(0,-2) and its $ e=\dfrac{1}{2} $ , then the equation of the directrix to the focus S is:
(a) x-y+3=0
(b) x-y+7=0
(c) x-y+5=0
(d) x-y+4=0

Answer 1

Hint: Start by using the property that the distance between the two foci of an ellipse is equal to twice the length of the semi-major axis multiplied by eccentricity. Also, the line passing through the two foci is the major axis and the directrix is perpendicular to the major axis, so use this to get the slope of the directrix. Finally, use the property that the distance between a focus and the corresponding directrix is equal to $ \dfrac{a}{e}-ae $ to get the answer.

Complete step-by-step answer:
Starting by drawing a rough diagram:

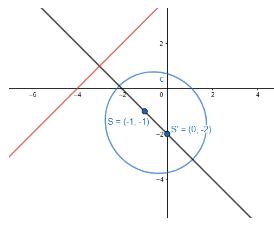
Now let us try to relate the diagram with the question.
From the figure, it is clear that the major axis of the ellipse is the line passing through the focus. So, let us find the equation of the major axis.
We know that the equation of the line passing through points $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ is given by:
 $ y=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)x+{{y}_{1}}-\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right){{x}_{1}} $ , where $ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} $ is the slope of the line. So, the equation of the major axis is:
 $ y=\left( \dfrac{-1-\left( -2 \right)}{-1-0} \right)x-2-0 $
 $ y=-x-2 $
Now we will find the slope of the line perpendicular to the major axis, as the directrix is also perpendicular to this line. We know that products of slopes of perpendicular lines are -1.
 $ \left( \text{slope of major axis} \right)\left( \text{slope of directrix} \right)=-1 $
 $ -1\left( \text{slope of directrix} \right)=-1 $
 $ \left( \text{slope of directrix} \right)=1 $
Therefore, using this slope, we can say that the equation of the directrix is:
 $ y=mx+c $
 $ \Rightarrow y=x+c $
 $ \Rightarrow x-y+c=0........(i) $
Where c is constant.
Now, we know that the distance between the two foci of an ellipse is equal to twice the length of the semi-major axis multiplied by eccentricity. Also, according to the distance formula, the distance between two points $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ is given by $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $ .
 $ SS'=\sqrt{{{\left( 0-\left( -1 \right) \right)}^{2}}+{{\left( -2-\left( -1 \right) \right)}^{2}}}=\sqrt{2} $
 $ \therefore 2ae=\sqrt{2} $
Now, we will put $ e=\dfrac{1}{2} $ . On doing so, we get
 $ 2a\times \dfrac{1}{2}=\sqrt{2} $
 $ a=\sqrt{2} $
Now, we know that the distance between a focus and the corresponding directrix is equal to $ \dfrac{a}{e}-ae $ to get the answer. Also, we know that the perpendicular distance of a point $ ({{x}_{1}},{{y}_{1}}) $ from the line $ ax+by+c $ is given by: $ \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} $ . So, here the point is S and the line is directrix.
 $ \dfrac{a}{e}-ae=\dfrac{-1-\left( -1 \right)+c}{\sqrt{{{1}^{2}}+{{\left( -1 \right)}^{2}}}} $
 $ \Rightarrow \dfrac{a}{e}-ae=\dfrac{c}{\sqrt{2}} $
If we substitute the value of a and e, we get
 $ \dfrac{\sqrt{2}}{\dfrac{1}{2}}-\sqrt{2}\times \dfrac{1}{2}=\dfrac{c}{\sqrt{2}} $
 $ \Rightarrow 2\times \sqrt{2}\times \sqrt{2}-\sqrt{2}\times \sqrt{2}\times \dfrac{1}{2}=c $
 $ \Rightarrow 4-1=3=c $
Putting the value back in equation (i), we get the equation of directrix to be x-y+3=0.
Hence, the answer to the above question is option (a).

Note: In such questions, the key is the diagram. If you get the diagram right, then you are most likely to reach an answer. Also, you must know the required formulas related to the conic and its elements which you are dealing with. The above question also required a good knowledge of perpendicular lines and distance between a point and a line.