Question

The given figure shows a pentagon ABCDE , EG drawn parallel to DA meets BA produced at G and CF drawn to DB meets AB produced at F.

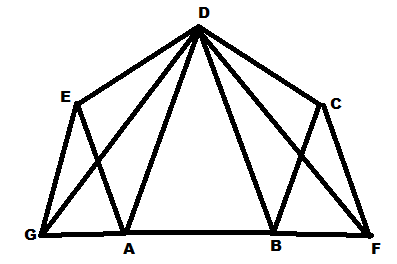
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

Answer 1

Hint:
By considering the triangles DGA and AED , DBC and BFD and using the property that the triangles having the same base and lie between the same parallel line have the same area we get two equations and adding the Area of $\vartriangle ABD$ on both sides we can get the required proof.

Complete step by step solution:

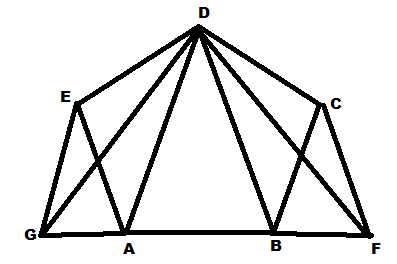
Let's consider the triangles DGA and AED
We can see that both the triangles have the same base AD and lie between the parallel lines AD and EG
So we get that
Area of $\vartriangle DGA$ = Area of $\vartriangle AED$………(1)
Now let's consider the triangles DBC and BFD
We can see that both the triangles have the same base DB and lie between the parallel lines BD and CF
So we get that
Area of $\vartriangle DBF$ = Area of $\vartriangle BCD$………(2)
Now by adding (1) and (2) we get
Area of $\vartriangle DGA$ + Area of $\vartriangle DBF$ = Area of $\vartriangle AED$ + Area of $\vartriangle BCD$
Now adding Area of $\vartriangle ABD$ on both sides
Area of $\vartriangle DGA$ + Area of $\vartriangle DBF$+ Area of $\vartriangle ABD$ = Area of $\vartriangle AED$ + Area of $\vartriangle BCD$+ Area of $\vartriangle ABD$………(3)
From the diagram we get that
Area of $\vartriangle DGA$= Area of $\vartriangle DGA$ + Area of $\vartriangle DBF$+ Area of $\vartriangle ABD$ …….. (4)
Area of pentagon ABCDE = Area of $\vartriangle AED$ + Area of $\vartriangle BCD$+ Area of $\vartriangle ABD$………(5)
Substituting (4) and (5) in (3) we get
Area of $\vartriangle DGA$= Area of pentagon ABCDE
Hence proved.

Note:
The sum of all the internal angles of a triangle is always $180^\circ$ no matter how the triangle is constructed.
The length of any side of a triangle is shorter than the sum of the other two sides.
A triangle can always be split into two right triangles no matter how the triangle is constructed.