
The given problem

Answer
501.6k+ views
Hint: In this problem we have to find the value of
Complete step-by-step answer:
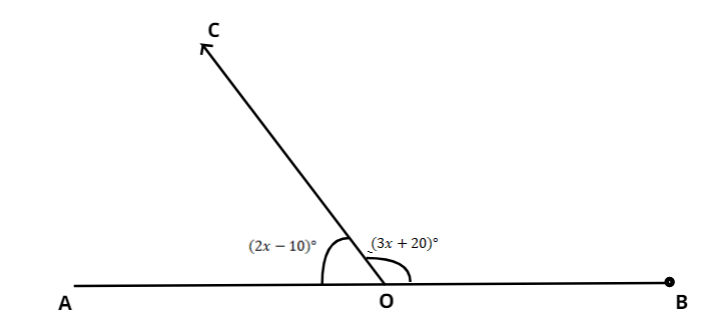
To solve the problem we have to draw the figure. Here
It is given that
Applying the property of straight angle, we have,
Putting the value of
Cancelling the degree sign from both sides,
After simplification, we obtain,
Solving for
So
Hence
Additional information: After finding the value of
Note: When one straight stands on another line it produces two adjacent angles. The sum of the two adjacent angles is always
Complete step-by-step answer:
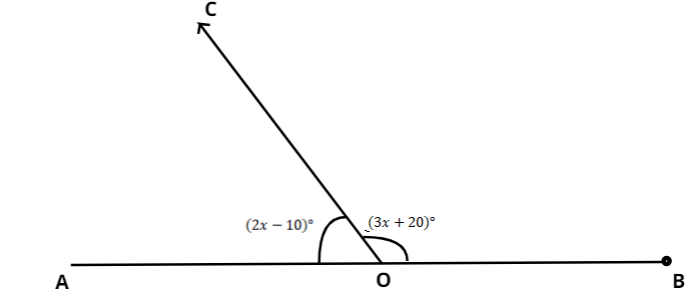
To solve the problem we have to draw the figure. Here

It is given that
Applying the property of straight angle, we have,
Putting the value of
Cancelling the degree sign from both sides,
After simplification, we obtain,
Solving for
So
Hence
Additional information: After finding the value of
Note: When one straight stands on another line it produces two adjacent angles. The sum of the two adjacent angles is always
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




