
The graph of quadratic polynomials is ___?
Answer
409.5k+ views
Hint: The graph obtained by plotting a quadratic polynomial comes out to be a Parabola . The roots obtained from solving the quadratic polynomial are the co – ordinates where the parabola cuts the X – Axis . This is because the roots are obtained by putting the given equation equal to zero i.e. where the value of the polynomial is zero .
Complete step-by-step answer:
We know that the standard form of parabola is equals to
This is shows it have real and distinct roots which are
and
Now , on plotting the graph of
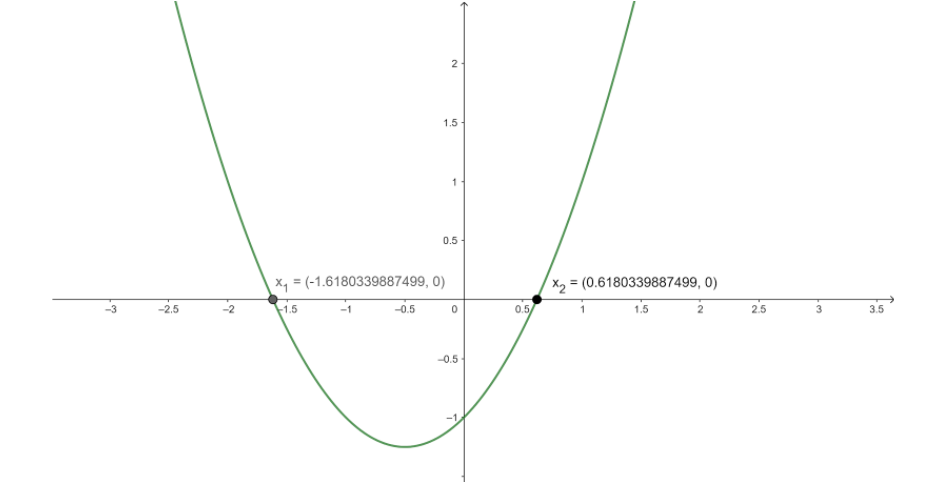
The intercepts at X – axis are roots of the equation . Also the graph of the equation symbolizes the shape of a parabola .
Note: The graph of a quadratic polynomial depends upon the degree of the polynomial such as if we have two variables with degree as
Complete step-by-step answer:
We know that the standard form of parabola is equals to
This is shows it have real and distinct roots which are
and
Now , on plotting the graph of

The intercepts at X – axis are roots of the equation . Also the graph of the equation symbolizes the shape of a parabola .
Note: The graph of a quadratic polynomial depends upon the degree of the polynomial such as if we have two variables with degree as
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




