Question

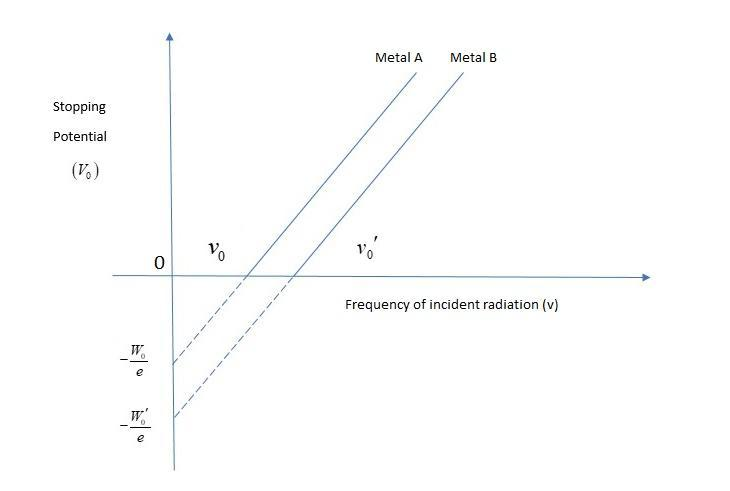
The graph shows variation of stopping potential ${V_0}$ versus frequency of incident radiation $\nu $ for two photosensitive metals $A$ and $B$. Which of the two metals have higher threshold frequency and why?

Answer 1

Hint: Stopping potential is always inversely proportional to work function of a metal. Work function$\phi $ of a metal gives us the threshold frequency (${\nu _0}$ ). Work function and threshold frequency are related as: $\phi = h{\nu _0}$ ,
where $h$ is the Planck's constant.
This gives us that work function is proportional to threshold frequency. So, we can easily conclude that stopping potential is directly proportional to threshold frequency. In the given graph, we are given the values of stopping potential for both the metals $A$ and $B$ for a given frequency of radiation falling on them. So, by knowing whose stopping potential has larger value, we can identify the metal having higher threshold frequency.

Complete step by step answer:
First of all, we should know what threshold frequency is. This is the minimum frequency of radiation which should be incident on the surface of metal to emit an electron out.
If the radiation having frequency higher than this is incident on the surface of the metal, then the ejected electron will also have some kinetic energy. This can be represented mathematically as
$h\nu - h{\nu _0} = {\text{Kinetic Energy}}$
Here, $h$ is the Planck's constant
${\nu _0}$ is the threshold frequency,
And $\nu $ is any frequency of incident radiation greater than threshold frequency.

Now, we need to define the term stopping potential. It is the potential required to stop the ejected electron with maximum kinetic energy. So, kinetic energy should be equal to the stopping potential so that the electron just stops. Kinetic energy of an electron is expressed as
${\text{Kinetic Energy}}=e{V_0}$
Where ${V_0}$ is the stopping potential.
Keeping this value of kinetic energy in the equation we already had, we get
$h\nu - h{\nu _0} = e{V_0}$

Now, for both the metals, frequency of incident radiation is the same. So, the term $h\nu $ is the same for both. So, we can easily conclude that more will be the magnitude of the term $e{V_0}$ , lesser will be the magnitude of the term $h{\nu _0}$ and vice-versa. From the graph, we can clearly see that the stopping potential of metal $A$ ( ${V_0}'$ ) is greater than the stopping potential of metal $B$ ( ${V_0}$ ).

So, by the conclusion made above, we can say that the threshold frequency of metal $A$ is lesser than the threshold frequency of metal $B$.
Hence, metal $B$ has higher threshold frequency.

Note: Here metal A and B have the same stopping potential at different frequencies, But Meta B has frequency more than metal A.
To solve such a similar question you should know the meaning of each symbol used in the graph and make conclusions. You can read the graph easily only if you know the equations used in sketching the graph.