
The height of a cone is 10cm. The cone is divided into two parts by drawing a plane through the midpoint of the axis of the cone, parallel to the base. Compare the volume of the two parts.
A.1 : 7
B.2 : 9
C.3 : 11
D.3 : 5
Answer
612.9k+ views
Hint: volume of a cone with radius r and height h is equal to $\dfrac{1}{3}\pi {r^2}h.$
Let the height of the given cone be h cm.
After dividing in two parts, we get
Resulting frustum has height half of the original cone and radius at the top of the frustum equal to half of the base radius of the cone.
Frustum of the cone with radius, R=10 cm and radius r = 5 cm, height = $\dfrac{h}{2}$ cm
A smaller cone of radius, r =(R/2) = 5 cm and height = $\dfrac{h}{2}$ cm
$\therefore $ Ratio of volumes = (volume of smaller cone) / (volume of frustum of cone)
$ = \dfrac{{\dfrac{1}{3}\pi {r^2}\left( {\dfrac{h}{2}} \right)}}{{\dfrac{1}{3}\pi \left( {\dfrac{h}{2}} \right)\left[ {{R^2} + {r^2} + Rr} \right]}}$
$ = \dfrac{{5 \times 5}}{{\left[ {{{10}^2} + {5^2} + 10 \times 5} \right]}} = \dfrac{{25}}{{175}}$
$ = \dfrac{1}{7}$
Therefore, 1:7 is the required ratio.
Note: we have to understand the given problem clearly. If we imagine the problem in geometric structure it is easy to solve. When we divide a cone as mentioned in the problem it looks similar to the below figure.
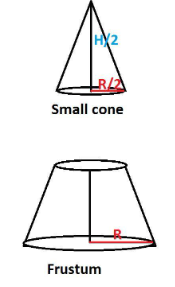
Let the height of the given cone be h cm.
After dividing in two parts, we get
Resulting frustum has height half of the original cone and radius at the top of the frustum equal to half of the base radius of the cone.
Frustum of the cone with radius, R=10 cm and radius r = 5 cm, height = $\dfrac{h}{2}$ cm
A smaller cone of radius, r =(R/2) = 5 cm and height = $\dfrac{h}{2}$ cm
$\therefore $ Ratio of volumes = (volume of smaller cone) / (volume of frustum of cone)
$ = \dfrac{{\dfrac{1}{3}\pi {r^2}\left( {\dfrac{h}{2}} \right)}}{{\dfrac{1}{3}\pi \left( {\dfrac{h}{2}} \right)\left[ {{R^2} + {r^2} + Rr} \right]}}$
$ = \dfrac{{5 \times 5}}{{\left[ {{{10}^2} + {5^2} + 10 \times 5} \right]}} = \dfrac{{25}}{{175}}$
$ = \dfrac{1}{7}$
Therefore, 1:7 is the required ratio.
Note: we have to understand the given problem clearly. If we imagine the problem in geometric structure it is easy to solve. When we divide a cone as mentioned in the problem it looks similar to the below figure.

Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who among the following opened first school for girls class 9 social science CBSE

What does the word meridian mean A New day B Midday class 9 social science CBSE

What is the full form of pH?

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it




