Question

The height of the tetrahedron whose adjacent edges are vectors $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ is:
(a)$6\sqrt{2}$
(b)$16\sqrt{3}$
(c)$12\sqrt{2}$
(d)$4\sqrt{\dfrac{2}{3}}$

Answer 1

Hint: The three vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ are forming a parallelepiped then we are going to find the volume of the parallelepiped. We are asked to find the height of the tetrahedron for that we need the volume of tetrahedron which we calculate by using the relationship between volume of parallelepiped and volume of tetrahedron which is equal to $\text{Volume of tetrahedron}=\dfrac{1}{6}\left( \text{Volume of parallelepiped} \right)$. The angles between the three vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ is $\dfrac{\pi }{3}$. Volume of parallelepiped is calculated by multiplying the scalar product of three vectors $\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]$ by itself. Height of the tetrahedron is calculated using the following formula $\text{Volume of tetrahedron}=\dfrac{1}{3}\left( \text{Area of base} \right)\left( \text{Height} \right)$. Area of base is calculated using the area of an equilateral triangle.

Complete step by step answer:
We have given the three vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ which are the adjacent edges of the tetrahedron.
In the below figure, we have drawn the parallelepiped form from the three vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ as follows:

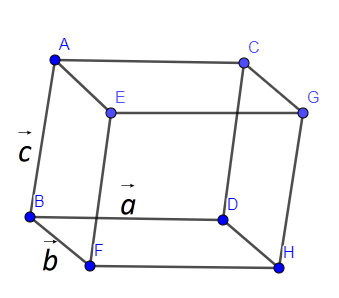
Volume of the above parallelepiped is equal to the scalar triple product of $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$.
As $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ are the adjacent sides of the tetrahedron so length of all the sides of this tetrahedron are equal and let us assume that the length of these three vectors as 4.
$\left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|=\left| \overrightarrow{c} \right|=4$
And angle between the three vectors as $\dfrac{\pi }{3}$.
Now, we can write the scalar triple product between $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ as:
$\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]$
The above scalar triple product is the volume of the parallelepiped which we are going to calculate by multiplying the scalar triple product by itself.
$\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]$
The multiplication of two scalar triple products is equal to:
$\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]=\left| \begin{matrix}
   \overrightarrow{a}.\overrightarrow{a} & \overrightarrow{b}.\overrightarrow{a} & \overrightarrow{c}.\overrightarrow{a} \\
   \overrightarrow{a}.\overrightarrow{b} & \overrightarrow{b}.\overrightarrow{b} & \overrightarrow{c}.\overrightarrow{b} \\
   \overrightarrow{a}.\overrightarrow{c} & \overrightarrow{b}.\overrightarrow{c} & \overrightarrow{c}.\overrightarrow{c} \\
\end{matrix} \right|$ ……….. Eq. (1)
We are now going to find the dot product of the three vectors taken two at a time.
$\overrightarrow{a}.\overrightarrow{a}=\overrightarrow{b}.\overrightarrow{b}=\overrightarrow{c}.\overrightarrow{c}=4.4=16$
The dot product of two different vectors is calculated as follows:
$\overrightarrow{a}.\overrightarrow{b}=\left| a \right|\left| b \right|\cos \theta $
In the above equation, $\theta $ is the angle between vector a and vector b. As we have shown above that angle between the vectors is equal to $\dfrac{\pi }{3}$. And the magnitude of all the vectors is equal and the value of the magnitude is 4.
$\begin{align}
  & \overrightarrow{a}.\overrightarrow{b}=\left( 4 \right)\left( 4 \right)\cos \dfrac{\pi }{3} \\
 & \overrightarrow{a}.\overrightarrow{b}=16\left( \dfrac{1}{2} \right)=8 \\
\end{align}$
Similarly, the dot product of the other different vectors taken two at a time is also 8.
$\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=8$
Substituting these dot products in eq. (1) we get,
$\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]=\left| \begin{matrix}
   16 & 8 & 8 \\
   8 & 16 & 8 \\
   8 & 8 & 16 \\
\end{matrix} \right|$
Solving the above determinant by taking 8 as common from each row then ${{8}^{3}}$ will comes outside from the determinant and we are left with:
$\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]={{8}^{3}}\left| \begin{matrix}
   2 & 1 & 1 \\
   1 & 2 & 1 \\
   1 & 1 & 2 \\
\end{matrix} \right|$
Expanding the determinant along first row we get,
$\begin{align}
  & \left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]={{8}^{3}}\left( 2\left( 2\left( 2 \right)-1\left( 1 \right) \right)-1\left( 1\left( 2 \right)-1\left( 1 \right) \right)+1\left( 1\left( 1 \right)-2\left( 1 \right) \right) \right) \\
 & \Rightarrow \left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]={{8}^{3}}\left( 2\left( 4-1 \right)-1\left( 2-1 \right)+1\left( 1-2 \right) \right) \\
 & \Rightarrow \left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]={{8}^{3}}\left( 2\left( 3 \right)-1\left( 1 \right)+1\left( -1 \right) \right) \\
 & \Rightarrow \left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]\left[ \begin{matrix}
   a & b & c \\
\end{matrix} \right]={{8}^{3}}\left( 4 \right)=2048 \\
\end{align}$
Volume of parallelepiped is equal to:
$\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]$
So, we have to take the square root of 2048 to get the volume of the parallelepiped.
$\left[ \begin{matrix}
   \overrightarrow{a} & \overrightarrow{b} & \overrightarrow{c} \\
\end{matrix} \right]=\sqrt{2048}=32\sqrt{2}$
In the below figure, we have shown a tetrahedron inside the parallelepiped:

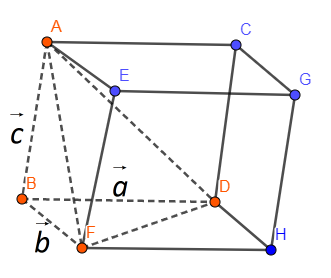
The dotted line in the above figure is the tetrahedron.
Now, the relationship between the volume of the parallelepiped and the tetrahedron is given as:
$\text{Volume of tetrahedron}=\dfrac{1}{6}\left( \text{Volume of parallelepiped} \right)$
Substituting the volume of parallelepiped as $32\sqrt{2}$ in the above equation we get,
$\text{Volume of tetrahedron}=\dfrac{1}{6}\left( 32\sqrt{2} \right)=\dfrac{16\sqrt{2}}{3}$
Now, the volume of tetrahedron is equal to:
$\dfrac{1}{3}\left( \text{Area of base} \right)\left( \text{height} \right)$
Area of base of the tetrahedron is an equilateral triangle with a side length as 4 and we know the formula for area of equilateral triangle as:
$\begin{align}
  & \dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}} \\
 & =\dfrac{\sqrt{3}}{4}{{\left( 4 \right)}^{2}}=4\sqrt{3} \\
\end{align}$
The above calculation gives us the area of base as $4\sqrt{3}$. Now, substituting this area of base in the formula of volume of tetrahedron we get,
$\dfrac{1}{3}\left( 4\sqrt{3} \right)\left( \text{height} \right)$
Now, we have solved the volume of tetrahedron as $\dfrac{16\sqrt{2}}{3}$ so equating the above expression to this value of volume we get,
$\dfrac{1}{3}\left( 4\sqrt{3} \right)\left( \text{height} \right)=\dfrac{16\sqrt{2}}{3}$
Solving the above equation we get,
$\begin{align}
  & \left( 4\sqrt{3} \right)\left( \text{height} \right)=16\sqrt{2} \\
 & \Rightarrow \left( \text{height} \right)=\dfrac{16\sqrt{2}}{4\sqrt{3}}=4\sqrt{\dfrac{2}{3}} \\
\end{align}$
Hence, we got the value of height of the tetrahedron as $4\sqrt{\dfrac{2}{3}}$.

So, the correct answer is “Option D”.

Note: You might have thought why we have chosen 4 as the length of the three vectors, we can take some random constant “a” also so the answer is you can take any constant and then substitute “a” in place of magnitude of the vectors in the above calculation, you will get the same answer as we are getting above.
The following information that you extract from this problem which you can apply in the other problems as well:
The volume of parallelepiped, volume of tetrahedron, relationship between volume of tetrahedron and volume of parallelepiped and relationship between volume of tetrahedron, area of base and height of the tetrahedron.