Question

The horizontal component of earth’s magnetic field at a place is $\dfrac{1}{{\sqrt 3 }}$times the vertical component. Determine the angle of dip at that place.

Answer 1

Hint: At any place, the earth’s magnetic field always has two components, one is horizontal and other is vertical component and the angle between horizontal component and equivalent magnetic field is known as angle of dip. So, these quantities (viz. horizontal and vertical component and angle of dip) are dependent on each other. It means when the angle of dip changes then the horizontal and vertical components also change. So, with the help of trigonometric ratios we can calculate the unknown if two other parameters are given or there is a relation between two others.

Complete step-by-step solution -
Let,
At any place on the earth surface the equivalent magnetic field, its horizontal component, its vertical component and angle of dip are shown in the diagram as follows-

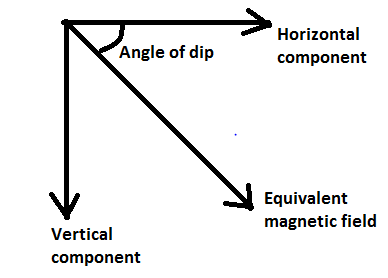
${{\text{B}}_e}$= Equivalent magnetic field
${{\text{B}}_h}$=Horizontal component
${{\text{B}}_v}$=vertical component
$\theta $=Angle of dip
Given,
It is given in the question that the Horizontal component of earth’s magnetic field at a place is $\dfrac{1}{{\sqrt 3 }}$times the vertical component,
So the mathematical expression showing the above relationship is as follows,
i.e. ${B_h} = \dfrac{1}{{\sqrt 3 }}{B_v}$-------equation(1)
 So,${B_v} = \sqrt 3 {B_h}$
By this we get a similar relationship between horizontal and vertical components, that is, here the vertical component is $\sqrt 3 $ times the horizontal component.
Now ,
We know the relation between these three (viz. horizontal component and vertical component and angle of dip) which is as follows(by taking the help of trigonometric ratio)
${\text{tan}}\theta {\text{ = }}\dfrac{{perpendicular}}{{base}}$
$\tan \theta = \dfrac{{{B_v}}}{{{B_h}}}$------- equation(2)
Now putting the value of ${{\text{B}}_v}$in equation no (2) from equation no (1),
\[\tan \theta = \dfrac{{\sqrt 3 {B_h}}}{{{B_h}}}\]
${\text{tan}}\theta {\text{ = }}\sqrt 3 $
So, $\theta = {60^ \circ }$
Hence the required angle of dip with respect to the above given situation is ${60^ \circ }$.

Note: At any place on the earth the angle between the horizontal component and the total magnetic field is known as angle of dip. So the magnetic field will be different at different places on the earth surface according to the change in magnitude of the magnetic field and the angle of dip.