
The horizontal component of the earth’s magnetic field at a place is B and the angle of dip is ${60^ \circ }$. What is the value of the vertical component of the earth’s magnetic field at the equator?
Answer
494.7k+ views
Hint: In this question, we start with the horizontal and vertical components of the earth’s magnetic field that is ${M_H} = M\cos \left( \delta \right)$ and ${M_V} = M\sin \left( \delta \right)$ respectively. Then we equate the horizontal component of the earth’s magnetic field to B and substitute $\delta = {60^ \circ }$ in ${M_H} = M\cos \left( \delta \right)$ and we get $M = 2B$. Now to find the vertical component of the magnetic field at the equator we substitute $M = 2B$ and $\delta = {60^ \circ }$ in ${M_V} = M\sin \left( \delta \right)$ and get ${M_V} = 0$ at the equator.
Complete step-by-step answer:
In this question, it is given that the horizontal component of the earth’s magnetic field at a location is $B$. Also, the dip at the same location is $\delta = {60^ \circ }$
So we first draw the figure shown below to have a better understanding
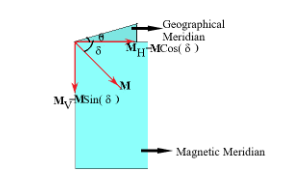
Now let us assume that the earth’s magnetic field $M$, so
The horizontal component will be ${M_H} = M\cos \left( \delta \right)$------ (1)
The vertical component will be ${M_V} = M\sin \left( \delta \right)$ -------- (2)
But it is given that horizontal component is $B$, so using equation (1) we get
${M_H} = M\cos \left( \delta \right) = B$------------------------------- (3)
Substituting $\delta = {60^ \circ }$ in equation (3), we will get
$B = M\cos \left( {{{60}^ \circ }} \right)$
$ \Rightarrow B = M \times \dfrac{1}{2}$
$ \Rightarrow M = 2B$ ------------------------------------- (4)
Now we know that at the equator the dip becomes zero, that is ${\delta _e} = {0^ \circ }$. So substituting ${\delta _e} = {0^ \circ }$ and $M = 2B$ in equation (2), we will get the vertical component of the magnetic field at the equator that is
${M_V} = M\sin \left( {{\delta _e}} \right)$
$ \Rightarrow {M_V} = 2B\sin \left( {{0^ \circ }} \right)$
$ \Rightarrow {M_V} = 2B \times 0$
$ \Rightarrow {M_V} = 0$
Hence the vertical component of the magnetic field at the equator of the earth is 0.
Note: For these types of questions we need to know what is Geographical meridian and magnetic meridian. We also need to know how to calculate the horizontal component and vertical component of the earth’s magnetic field. We should also know what is the angle of declination and angle of dip and how they vary at a different position on Earth’s surface.
Complete step-by-step answer:
In this question, it is given that the horizontal component of the earth’s magnetic field at a location is $B$. Also, the dip at the same location is $\delta = {60^ \circ }$
So we first draw the figure shown below to have a better understanding

Now let us assume that the earth’s magnetic field $M$, so
The horizontal component will be ${M_H} = M\cos \left( \delta \right)$------ (1)
The vertical component will be ${M_V} = M\sin \left( \delta \right)$ -------- (2)
But it is given that horizontal component is $B$, so using equation (1) we get
${M_H} = M\cos \left( \delta \right) = B$------------------------------- (3)
Substituting $\delta = {60^ \circ }$ in equation (3), we will get
$B = M\cos \left( {{{60}^ \circ }} \right)$
$ \Rightarrow B = M \times \dfrac{1}{2}$
$ \Rightarrow M = 2B$ ------------------------------------- (4)
Now we know that at the equator the dip becomes zero, that is ${\delta _e} = {0^ \circ }$. So substituting ${\delta _e} = {0^ \circ }$ and $M = 2B$ in equation (2), we will get the vertical component of the magnetic field at the equator that is
${M_V} = M\sin \left( {{\delta _e}} \right)$
$ \Rightarrow {M_V} = 2B\sin \left( {{0^ \circ }} \right)$
$ \Rightarrow {M_V} = 2B \times 0$
$ \Rightarrow {M_V} = 0$
Hence the vertical component of the magnetic field at the equator of the earth is 0.
Note: For these types of questions we need to know what is Geographical meridian and magnetic meridian. We also need to know how to calculate the horizontal component and vertical component of the earth’s magnetic field. We should also know what is the angle of declination and angle of dip and how they vary at a different position on Earth’s surface.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

What is a transformer Explain the principle construction class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE




