Question

The length, breadth and height of a cuboid are 12cm; 15cm and 6 cm respectively. The longest possible rod that can be kept inside the cuboid is of:

Answer 1

Hint: Cuboid: In geometry, a cuboid is a three-dimensional shape in which all sides are rectangles. It is a polyhedron, having 6 rectangular sides called faces, 8 vertices and 12 edges. These rectangular faces are at right angles to one another.
Thus, all angles in a cuboid are right angles.
The diagonal (d) of a cuboid is given as: \[d = \sqrt {{{(length)}^2} + {{(width)}^2} + {{\left( {height} \right)}^2}} \]

Complete step-by-step answer:
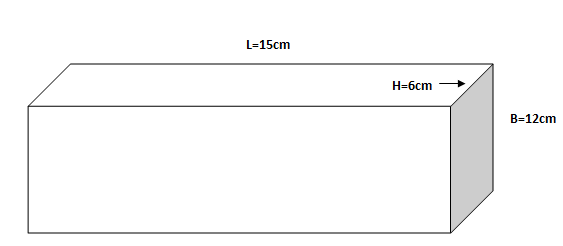
Given, length of a cuboid =15 cm
Breadth of a cuboid =12 cm
 Height of a cuboid =6 cm

As we know that the longest rod that can be kept inside the cuboid will be the diagonal (d) of the cuboid.
\[ \Rightarrow \]\[ d = \sqrt {{{(length)}^2} + {{(width)}^2} + {{\left( {height} \right)}^2}} \]
\[ \Rightarrow d = \sqrt {{{(15)}^2} + {{(12)}^2} + {{\left( 6 \right)}^2}} \]
\[ \Rightarrow d = \sqrt {225 + 144 + 36} \]
\[ \Rightarrow d = \sqrt {405} \]
\[ \Rightarrow d = 9\sqrt 5 cm\]
Required length of the longest rod that can be kept inside the given cuboid will be \[9\sqrt 5 cm\].
Note: Whenever we have given a cuboid, the longest length in the cuboid is its diagonals.
If someone asks to find the length of the longest length in the cuboid find the diagonal of the cuboid using formula\[ = \sqrt {{{(length)}^2} + {{(width)}^2} + {{\left( {height} \right)}^2}} \].