Question

The length of one side of a rhombus is 3.5 cm and its altitude is 10 cm. If the length of one of its diagonals is 26 cm, what will be the length of the other diagonal?
a) 5 cm
b) 10 cm
c) 8 cm
d) 6cm

Answer 1

Hint: Area of the rhombus in terms of base and height is given as; $\text{Any side}\times \text{corresponding altitude}$ . Area of rhombus in terms of the diagonals can be given as
$\dfrac{1}{2}\times {{\left( \text{diagonal} \right)}_{1}}\times {{\left( \text{diagonal} \right)}_{2}}$ use both the identities to get the area of rhombus and equate them to get the unknown diagonal.

Complete step by step answer:
Here, it is given that the length of an altitude on the side of rhombus of length 6.5 cm, is 10 cm. And we need to determine the length of a diagonal if the length of another diagonal is 26 cm. so, we can draw an sketch as

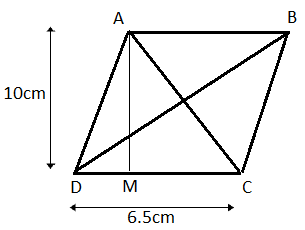
So, let us suppose a Rhombus ABCD with side DC = 6.5 cm and altitude AD is of length 10 cm on it. And we need to determine length BD if AC = 26 cm. We know the area of rhombus can be given two ways. One in form of base and corresponding height and another in terms of both the diagonals. So, both can be given as
$\begin{align}
  & \text{Area of rhombus}=\text{side}\times \text{corresponding altitude} \\
 & \text{Area of rhombus = }\dfrac{1}{2}\times {{\left( \text{diagonal} \right)}_{1}}\times {{\left( \text{diagonal} \right)}_{2}} \\
\end{align}$
So, area with side DC and AM as a corresponding altitude from the first relation of the area can be given as
Area of rhombus ABCD $=6.5\times 10=65c{{m}^{2}}$
Similarly, area of rhombus with the help of diagonals BD and AC can be given from the second relation as
Area of rhombus ABCD $=\dfrac{1}{2}\times 26\times BD$
So, equating both the areas calculated above, as both are representing the area of rhombus ABCD. Hence we get
$\begin{align}
  & 65=\dfrac{1}{2}\times 26\times BD \\
 & \dfrac{65}{13}=BD \\
 & BD=5cm \\
\end{align}$
Hence, the length of the other diagonal is 5 cm.
So option (a) is correct.

Note: Area of rhombus can be given in terms of diagonals and side corresponding altitude as well. We need to know both the identities to solve this kind of question. One may confuse with the properties of diagonals of the rhombus and may give length another diagonal as 26 cm as well. As he or she may think that rhombus has equal diagonals. But it’s not true, Diagonals of rhombus are not equal to each other. Rectangle and square have equal diagonals only. So be careful with the properties of the rhombus as well.