Question

The length of the longest pole that can be put in a room of dimensions 10m×10m×5m is:
(a)15m
(b)16m
(c)10m
(d)12m

Answer 1

Hint: We have to find the length of a longest pole means the longest distance in a room. As it is given that room is in the form of cuboid so the longest length of a line in the cuboid is a diagonal of the cuboid.

Complete step-by-step answer:
The dimensions of a room given in the question are in the form of a cuboid i.e. (10m×10m×5m).
Now, in the question it is asked that we have to fit the longest pole in the cuboid. It means we need to find the space in a cuboid which can accommodate the longest pole.
In a cuboid, the longest length is the diagonal of a cuboid. So, if we know the diagonal of a cuboid we can fit the longest pole there.

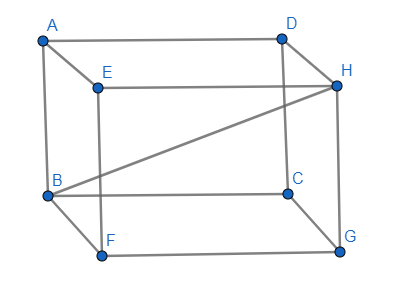
In the above figure, BH is the diagonal of a cuboid.
A cuboid having length = l, breadth = b, height = h then the formula of the diagonal of a cuboid is:
$\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$
And the dimensions of a room are given as 10m×10m×5m where l = 10m, b = 10m and c = 5m then substituting the values of l, b and h in the above expression we get,
$\begin{align}
  & \sqrt{{{\left( 10 \right)}^{2}}+{{\left( 10 \right)}^{2}}+{{\left( 5 \right)}^{2}}} \\
 & =\sqrt{100+100+25} \\
 & =\sqrt{225} \\
 & =15 \\
\end{align}$
From the above calculations, the length of the diagonal is 15m.
Hence, the longest pole which can be put in a room is 15m.
Hence, the correct option is (a).
Note: Don’t forget to write the units of length. And the derivation for the length of the diagonal is given below:
Imagine you are sitting in a room then “l” is the length of the floor and “b” is the breadth of the floor then the length of the diagonal of a floor is$\sqrt{{{l}^{2}}+{{b}^{2}}}$. Now, you can imagine a right angled triangle whose base is the diagonal of a floor and height is the height of the room “h” and hypotenuse is the diagonal of a room so applying Pythagoras theorem on this right angled triangle.
Hence, diagonal of a room is $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$