Question

The midpoint of side BC of triangle ABC, with A (1, -4) and the mid-points of the sides through A being (2, -1) and (0, -12) is

Answer 1

Hint: In the above question we have a triangle ABC in which D, E, and F are midpoints. Side AB has a mid-point D, Side AC has a midpoint E, and Side BC has a midpoint F. Co-ordinate of A, D, and E is given. We will use the midpoint formula to solve this question.

Complete step-by-step answer:
Drawing figure from the given data:
     

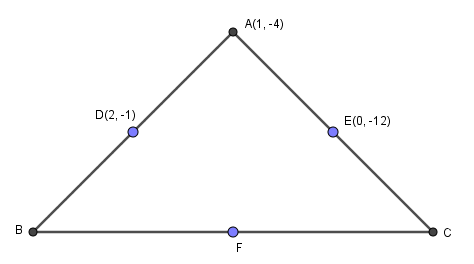
From the figure, we know that;
D is the midpoint of AB.
E is the midpoint of AC.
F is the midpoint of BC.
In triangle ABC,
Coordinates of A (1, -4)
Coordinates of D (2, -1)
Coordinates of E (0, -12)
We need to find the Coordinates of F which is a midpoint of BC.
Let the Coordinates of B be $\left( {{x_2},{y_2}} \right)$, C be $\left( {{x_3},{y_3}} \right)$, and F be $\left( {x,y} \right)$.
Now, using midpoint formula, we will try to find the coordinates of B
Coordinates of B $ = \dfrac{{1 + {x_2}}}{2} = 2$ and $\dfrac{{ - 4 + {y_2}}}{2} = - 1$
After solving above equation, we get;
Coordinates of B (3, 2)
Now, using midpoint formula, we will try to find the coordinates of C
Coordinates of C $ = \dfrac{{1 + {x_3}}}{2} = 0$ and $\dfrac{{ - 4 + {y_3}}}{2} = - 12$
After solving above equation, we get;
Coordinates of C (-1, -20)
Now, using midpoint formula, we will try to find the coordinates of F
Coordinates of F $ = \dfrac{{{x_2} + {x_3}}}{2} = x$ and $\dfrac{{{y_2} + {y_3}}}{2} = y$
Putting the values in the above equations, we get;
$ = \dfrac{{3 - 1}}{2} = x$ and $\dfrac{{2 - 20}}{2} = y$
After solving above equation, we get;
Coordinates of F (1, -5)

Note: In this type of problems usually students make mistakes by considering the end point coordinates as equals to the sum of another endpoint and midpoint coordinates. The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.