Question

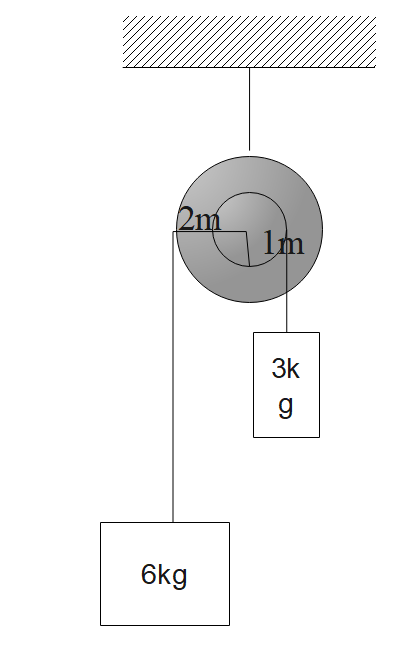
The moment of inertia of the pulley system in the figure is $3kg{{m}^{2}}$. The radii of bigger and smaller pulleys are two and one meter respectively. As the system is released from rest, find the angular acceleration of the pulley system.

Answer 1

Hint: Calculate the net force acting on the two masses without considering the rotational forces. Next, find out the torque equation about the pulley for both the ropes. Now, substitute the tension values of two blocks from the first equation to the torque equation that we got. We can substitute the rest of all values given in the question and find out the angular acceleration of the pulley.
Formula used:
$\begin{align}
  & T=Mg-Ma \\
 & I\alpha ={{T}_{1}}{{r}_{1}}-{{T}_{2}}{{r}_{2}} \\
\end{align}$

Complete answer:
Let us write down the given values,
The masses of the blocks, radius of the ropes, tension in the ropes, angular acceleration and linear acceleration as $M=6kg,m=3kg,{{r}_{1}}=2m,{{r}_{2}}=1m,{{T}_{1}}-6kg,{{T}_{2}}-3kg,\alpha ,a$.
Now, the net force acting on the heavier block is equal to,
$\begin{align}
  & Mg-{{T}_{1}}=Ma \\
 & {{T}_{1}}=Mg-Ma \\
\end{align}$
Next, the net force acting on the lighter block is,
$\begin{align}
  & {{T}_{2}}-mg=ma \\
 & {{T}_{2}}=mg+ma \\
\end{align}$
Consider rotational motion,
Torque equation about the pulley is given as,
$\begin{align}
  & I\alpha ={{T}_{1}}{{r}_{1}}-{{T}_{2}}{{r}_{2}} \\
 & I\alpha =(Mg-Ma){{r}_{1}}-(mg+ma){{r}_{2}} \\
 & 3\alpha =(6(9.8)-6({{r}_{1}}\alpha )){{r}_{1}}-(3(9.8)+3({{r}_{2}}\alpha )){{r}_{2}} \\
 & \alpha =2.94rad{{s}^{-1}} \\
\end{align}$
therefore, the angular acceleration is $2.94rad{{s}^{-1}}$.

Additional Information:
Moment of inertia is the ratio of net angular momentum of a given system to its angular velocity around a principal axis. It means that, if the angular momentum of any system is constant, as the moment of inertia decreases, the angular velocity must eventually be increased. Moment of inertia is important because it is used to calculate angular momentum and allows to explain how rotational motion changes when mass distribution of mass changes. If the moment of inertia is high, it means that a higher force must be applied in order to cause a rotation to the object. Masses that are really far away from the axis of rotation have the greatest moment of inertia as the distance between object and axis of rotation increases.

Note:
The values of moment of inertia for some standard shapes are only true if the axis of rotation goes through the center of mass in the direction indicated. For any axis of rotation located at different points, we can use the parallel axis theorem and find the correct value. This is only applicable if the direction of rotation is the same. For different directions of rotation, the moment of inertia is completely different.