Question

The moment of inertia of uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the centre is :
$\text{A}\text{. }\dfrac{1}{4}M{{r}^{2}}$
$\text{B}\text{. }\dfrac{2}{5}M{{r}^{2}}$
$\text{C}\text{. }M{{r}^{2}}$
$\text{D}\text{. }\dfrac{1}{2}M{{r}^{2}}$

Answer 1

Hint: Consider a thin semicircular ring of radius x and width dx of the disc, whose centre is the same as that of the disc. Let the mass of this ring be dm. The moment of inertia of this ring is given as $dI=dm{{x}^{2}}$. Find the value of dm in terms of x. Then integrate the equation to get the value of the moment of inertia of the half-disc about the given axis.

Formula used:
$I=m{{r}^{2}}$

Complete answer:
A semicircular disc is made up of multiple concentric semicircular rings. Consider a thin semicircular ring of radius x and width dx of the disc, whose centre is the same as that of the disc. Let the mass of this ring be dm.

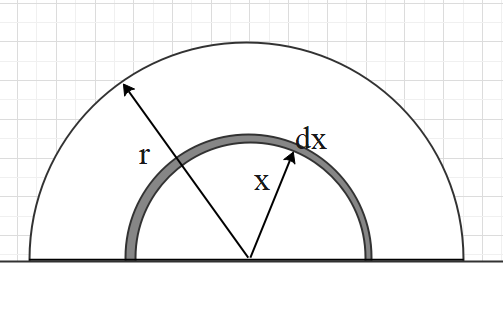
The moment of inertia of a semicircular ring about a line perpendicular to the plane of the ring through its centre is given as $I=m{{r}^{2}}$, where m and r are the mass and radius of the ring.
In this case, the mass of the half-ring is dm and its radius is x. Let its moment of inertia be dI.
Therefore, $dI=dm{{x}^{2}}$ …. (i).
dI is the moment of inertia of the thin ring about the given axis. If we find the sum of all the half-rings of the semicircular disc, we will find the moment of inertia of the disc about the given axis.
Therefore, we have to integrate dI with respect to dr with the limit from x=0 to x=r.
Before that we have substituted dm in equation (i).
For that we will use the uniform areal density of the disc.
This means that the real density of the disc and the thin ring will be the same.
The areal density of the disc is $\sigma =\dfrac{M}{\dfrac{1}{2}\pi {{r}^{2}}}=\dfrac{2M}{\pi {{r}^{2}}}$
The ring is of width dx and its length is $l=\pi x$. Therefore, the area of this half-ring will be length times width.

Therefore areal density of the ring is $\sigma =\dfrac{dm}{\pi xdx}$
Therefore, $\sigma =\dfrac{2M}{\pi {{r}^{2}}}=\dfrac{dm}{\pi xdx}$
$\Rightarrow dm=\dfrac{2Mxdx}{{{r}^{2}}}$.
Substitute the value of dm in equation (i).
 $\Rightarrow dI=\left( \dfrac{2Mxdx}{{{r}^{2}}} \right){{x}^{2}}$
$\Rightarrow dI=\dfrac{2M}{{{r}^{2}}}{{x}^{3}}dx$
Integrate both the sides with mentioned limits of x.
$\Rightarrow \int{dI}=\dfrac{2M}{{{r}^{2}}}\int\limits_{0}^{r}{{{x}^{3}}dx}$
$\Rightarrow I=\dfrac{2M}{{{r}^{2}}}.\left. \dfrac{{{x}^{4}}}{4} \right|_{0}^{r}=\dfrac{2M}{{{r}^{2}}}\left( \dfrac{{{r}^{4}}}{4}-\dfrac{{{0}^{4}}}{4} \right)=\dfrac{2M}{{{r}^{2}}}\dfrac{{{r}^{4}}}{4}=\dfrac{M{{r}^{2}}}{2}$.
Therefore, the moment of inertia of the semi-circular disc about an axis perpendicular to its plane and passing through its centre is equal to $\dfrac{M{{r}^{2}}}{2}$.

So, the correct answer is “Option C”.

Note:
We can find the moment of inertia of the half-disc about the given axis in a shorter way if we know the moment of inertia of the whole ring of mass 2M about the same axis.
The moment of inertia of a circular disc about an axis perpendicular to its plane and passing throug its centre is equal to $\dfrac{M{{r}^{2}}}{2}$, where M is the mass of the disc and r is the radius of the disc. In this case the mass of the disc is 2M.

Hence, the moment of inertia of the complete disc is $\dfrac{(2M){{r}^{2}}}{2}=M{{r}^{2}}$.
This disc is made up of two semi-circular discs of masses M each. Due to symmetry both the half-discs will have the same moment of inertia. Let the moment of inertia of each half-disc about the given axis be I.
Now, the sum of the moment of inertia of these two half-discs is equal to the moment of inertia of the complete.
This means that $I+I=M{{r}^{2}}$
$\Rightarrow 2I=M{{r}^{2}}$
$\Rightarrow I=\dfrac{M{{r}^{2}}}{2}$.