Question

The number of divisors of 3630, which have a remainder of 1 when divided by 4, is

A) 12
B) 6
C) 4
D) None of these

Answer 1

Hint: First, we will find the prime factorization of the given number. Then we will find the possible divisors from the obtained prime factorization. Apply the given condition from the question to find the required value.

Complete step by step solution: We are given that the number is 3630.

We know that the prime factorization is finding which prime number multiplies together to make the original number.

We will now find the prime factorization of the given number 3630 by finding the prime numbers, which are divisible by this number.

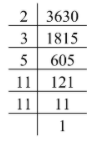
Thus, the prime factorization of the given number 3630 is \[2 \times 3 \times 5 \times {11^2}\].

We will now require such divisors, which have a remainder of 1 when divided by 4.

Finding the odd divisors from the above prime factorization of the given number 3630, we get

\[2, 3, 5, 11, {11^2}\]

We will now find the possible divisors of the given number 3630 from the above odd divisors.

1
\[1 \times 3 = 3\]
\[1 \times 5 = 5\]
\[1 \times 11 = 11\]
\[1 \times 121 = 121\]
\[3 \times 5 = 15\]
\[3 \times 11 = 33\]
\[3 \times 121 = 363\]
\[5 \times 11 = 55\]
\[5 \times 121 = 605\]

Finding the remainder by dividing each of the above possible divisors of the given number 3630 with 4, we get

1
3
1
3
1
3
1
1
3
1


Thus, the divisors of the given number are 1, 5, 121, 33, 363, 605, which leaves a remainder 1 when divided by 4.

Therefore, there are only 6 possible divisors, which leave a remainder 1 when divided by 4.

Hence, the option B will be correct.


Note: In this question, we will use the prime factorization method by finding the prime numbers, which multiply together to make the original number. While solving these types of questions, some students take the prime factors of the given number as the divisors, which is wrong. We will find the remainders by dividing the divisors separately. Then find the number of those divisors, which leaves the remainder 1.