Question

The number of lines of symmetry in a regular polygon of \[n\] sides is ____________
A. \[n\]
B. 1
C. 2
D. 3

Answer 1

Hint: In this question, we will proceed by defining what are lines of symmetry and then consider some examples of regular polygons such as triangle, square, pentagon and hexagon. Then observe the sequence and try to get the logic in lines of symmetry to get the required answer. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
The line of symmetry is the imaginary line where you could fold the image and have both halves match exactly.
Let us consider the lines of symmetry for some of the polygons as shown in the below figure:

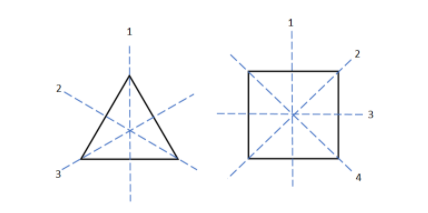
For triangle, \[n = 3\] and lines of symmetry = 3
For square, \[n = 4\] and lines of symmetry = 4
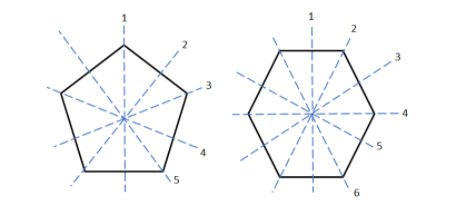
For pentagon, \[n = 5\] and lines of symmetry = 5
For hexagon, \[n = 6\] and lines of symmetry = 6
So, we can observe that lines of symmetry for a regular polygon is equal to the number of sides of that polygon.
Therefore, for a polygon with \[n\] sides, lines of symmetry = \[n\]
Thus, the correct option is A. \[n\]

Note: Lines of symmetry or reflection symmetry or line symmetry or mirror symmetry all are same. A regular polygon is a polygon that is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Remember that for a regular polygon the lines of symmetry are equal to the number of sides of the polygon.