Question

The number of vertices in a cube is
A. 6
B. 10
C. 8
D. 12

Answer 1

Hint: In order to solve the problem students may use the Euler’s formula for the calculation of vertex or directly draw the figure and count for the vertex.

Complete Step-by-Step solution:
Method (I)
Let us count the vertex from the figure of a cube.

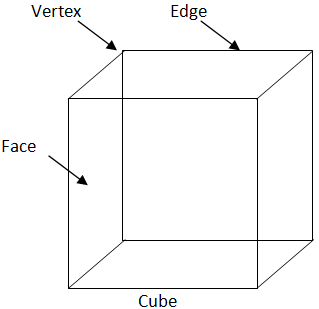
Given figure is a cube. For the figure one of the vertices is mentioned in the figure.
Vertices or a vertex is the technical term used in geometry for the corner points of a solid shape.
As we can see there are 8 similar corners of this solid shape. So there are 8 vertices.
Method (II)
Also by Euler’ formula.
Euler's formula is usually presented as follows: Faces + Vertices - Edges = 2 However, the formula can be rearranged to make the number of vertices the subject of the formula.
Rearrange the formula as follows: Add the Edges to each side of the equation to get: Faces + Vertices = Edges + 2 Now subtract the Faces from each side of the equation to get: Vertices = Edges + 2 – Faces.
As we know that for the cube.
No of edges = 12
No of faces = 6
So, no of vertices = 12 + 2 – 6 =8
By both methods the answer is the same.
Hence the number of vertices in a cube are 8.
So, option C is the right option.

Note: A cube is a region of space formed by six identical square faces joined along their edges. Three edges join at each corner to form a vertex. The cube can also be called a regular hexahedron. It is one of the five regular polyhedrons, which are also sometimes referred to as the Platonic solids. Students may use any of the methods shown above to find the number of vertices. But counting the vertices from the figure is quite easier.