Question

The opposites sides of a rectangle are equal
\[\begin{align}
  & (A)\text{ True}\text{.} \\
 & (B)\text{ False}\text{.} \\
 & (C)\text{ Only when rectangle is a square}\text{.} \\
 & (D)\text{ None of these}\text{.} \\
\end{align}\]

Answer 1

Hint: We know that a rectangle is also a parallelogram. So, the properties of parallelogram can be implied to properties of rectangles. We have to construct a diagonal to the parallelogram. This diagonal divides the parallelogram into 2 triangles. By applying the concept of alternate angles, obtain a concurrency between the 2 triangles. By using the concurrency relation, we can determine whether opposite sides of the rectangle are equal or not.

Complete step-by-step answer:
Consider a 4-sided polygon as shown below. We know that a 4-sided polygon is also called a quadrilateral.
PARALLELOGRAM: A parallelogram is said to be a quadrilateral whose opposite sides are parallel.

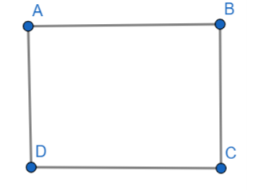
If ABCD is a parallelogram, then opposite sides of ABCD must be parallel.
In the parallelogram ABCD, the opposite side of side AB is side CD.
Hence, side AB must be parallel to side CD.
\[AB||CD.......(1)\]
In the similar manner, in parallelogram ABCD, the opposite side of side AD is side BC.
Hence, side AD must be parallel to side BC.
\[AD||BC......(2)\]

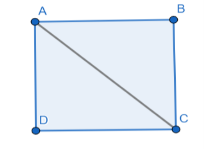
Let us join the points A and C in parallelogram ABCD as shown in above figure.
From equation (1),
We know that \[AB||CD\].

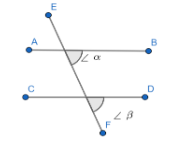
Let AB and CD are two parallel lines. Assume a transverse line EF intersecting both AB and CD.
Assume EF makes an angle \[\alpha \]with AB and makes an angle \[\beta \] with CD.
 \[\begin{align}
  & \angle BAF=\alpha ......(3) \\
 & \angle DCF=\beta ......(4) \\
\end{align}\]
These angles \[\alpha \] and \[\beta \] are said to be alternate angles.
We know that alternate angles are equal.
Hence,
\[\begin{align}
  & \angle BAF=\angle DCF \\
 & \Rightarrow \alpha =\beta \\
\end{align}\]
We need to apply the same scenario in parallelogram ABCD.
\[\begin{align}
  & \angle DAC=\angle ACB.....(5) \\
 & \angle DCA=\angle CAB......(6) \\
\end{align}\]
Now, we are having two triangles in the above parallelogram. One triangle is \[\Delta ABC\] and the other triangle is \[\Delta ACD\].
From equation (5) and equation (6)
\[\begin{align}
  & \angle DAC=\angle ACB \\
 & \angle DCA=\angle CAB \\
\end{align}\]
AC is the common side.
Hence by S.A.S axiom, \[\Delta ABC\] and \[\Delta ACD\] are congruent.
From the triangles \[\Delta ABC\] and \[\Delta ACD\],
\[\begin{align}
  & AB=CD......(7) \\
 & AD=BC.......(8) \\
\end{align}\]
We already know that (AB, CD) and (AD, BC) are pairs of opposite sides of a given parallelogram.
From (7) and (8),
It is clear that the lengths of opposite sides of a parallelogram are equal.
We know that a rectangle is also a parallelogram.
Hence, the opposite sides of a rectangle are equal.
Therefore, option (A) is correct.

Note: We can solve this in another way also.
Let us assume a parallelogram ABCD as shown in below figure.

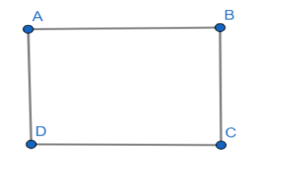
From the diagram, it is clear that (AB, CD) and (AD, BC) are two pairs of opposite sides.
Now join vertex A and vertex C to form a diagonal AC as shown in below figure.

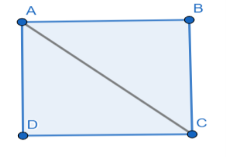
We know that a diagonal of quadrilateral divides the quadrilateral into two congruent triangles.
As parallelogram is also a quadrilateral, the diagonal AC divides the parallelogram ABCD into two congruent triangles. The two congruent triangles are \[\Delta ABC\] and \[\Delta ADC\].
As \[\Delta ABC\] and \[\Delta ADC\] are congruent,
AB and CD are said to be of equal lengths.
In the similar manner, AD and BC are also said to be of equal lengths.
So, we can say that the opposite sides of parallelograms are equal.
We know that a rectangle is a parallelogram if the angle between adjacent sides of the parallelogram is the right angle. Hence, we can say that the opposite sides of the rectangle are equal.