Question

The orthocenter of the triangle formed by \[\left( {8,0} \right)\] and \[\left( {4,6} \right)\] with the origin is:
A.\[\left( {4,\dfrac{8}{3}} \right)\]
B.\[\left( {3, - 4} \right)\]
C.\[\left( {4,3} \right)\]
D.\[\left( {3,4} \right)\]

Answer 1

Hint: Here, we will find the orthocenter of the triangle. First, we will be finding the slope of the altitudes of a triangle by using the slope formula. Then by using the equation of a line we will find the equation of the altitudes of a triangle. We will solve the equations of two altitudes of a triangle to find the point of intersection that is the orthocenter. Orthocenter is defined as the point of intersection of the altitudes of a triangle.

Formula Used:
We will use the following formulas:
1. Slope of the line is given by the formula \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] .
2. Slope of two perpendicular lines \[{m_1} \times {m_2} = - 1\] .
3. Equation of the line with a point and slope is given by the formula \[y - {y_1} = m\left( {x - {x_1}} \right)\].

Complete step-by-step answer:
We will first draw the diagram based on the given information.

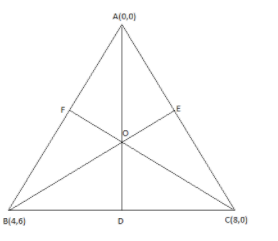
Let ABC be the vertices of the triangle. Let the coordinates of A, B, C be \[\left( {0,0} \right),\left( {4,6} \right),\left( {8,0} \right)\]. respectively. Let AB, BE, CF be the altitudes of the triangle ABC of the sides BC, CA, AB respectively. Let O be the orthocenter of the triangle.
Consider any two altitudes AD, CF of the triangle ABC.
Now, we will find the slope of the line \[C\left( {8,0} \right)\]and \[B\left( {4,6} \right)\].
Now we will find the Slope of the line BC .
Substituting \[{x_1} = 8\], \[{x_2} = 4\], \[{y_1} = 0\] and \[{y_2} = 6\] in the formula \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\], we get
\[{m_{BC}} = \dfrac{{6 - 0}}{{4 - 8}}\]
Subtracting the terms, we get
 \[ \Rightarrow {m_{BC}} = \dfrac{6}{{ - 4}}\]
Dividing numerator and denominator by 2, we get
\[ \Rightarrow {m_{BC}} = \dfrac{{ - 3}}{2}\]
We know that slope of two perpendicular lines \[{m_1} \times {m_2} = - 1\].
Since the line AD is perpendicular to the line BC, so we get
\[\begin{array}{l}{m_{AD}} \times {m_{BC}} = - 1\\ \Rightarrow {m_{AD}} \times \dfrac{{ - 3}}{2} = - 1\end{array}\]
On cross multiplication, we get
\[ \Rightarrow {m_{AD}} = - 1 \times \dfrac{{ - 2}}{3}\]
Multiplying the terms, we get
\[ \Rightarrow {m_{AD}} = \dfrac{2}{3}\]
Equation of the line AD is given with the point \[A\left( {0,0} \right)\] with slope \[\dfrac{2}{3}\] .
So, using the formula \[y - {y_1} = m\left( {x - {x_1}} \right)\], we get
 \[ \Rightarrow y - 0 = \dfrac{2}{3}\left( {x - 0} \right)\]
\[ \Rightarrow y = \dfrac{2}{3}x\] …………………………………………………………………………..\[\left( 1 \right)\]
Now, we will find the slope of the line \[B\left( {4,6} \right)\]and\[A\left( {0,0} \right)\].
Substituting \[{x_1} = 0\], \[{x_2} = 4\], \[{y_1} = 0\] and \[{y_2} = 6\] in the formula \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\], we get
Slope of the line AB\[{m_{AB}} = \dfrac{{6 - 0}}{{4 - 0}}\]
Subtracting the terms, we get
\[ \Rightarrow \] Slope of the line AB\[{m_{AB}} = \dfrac{6}{4}\]
Dividing numerator and denominator by 2, we get
\[ \Rightarrow \] Slope of the line AB\[{m_{AB}} = \dfrac{3}{2}\]
Slope of two perpendicular lines \[{m_1} \times {m_2} = - 1\]
Since the line CF is perpendicular to the line AB, so we get
\[\begin{array}{l}{m_{BE}} \times {m_{AB}} = - 1\\ \Rightarrow {m_{BE}} \times \dfrac{3}{2} = - 1\end{array}\]
On cross multiplication, we get
\[ \Rightarrow \] \[{m_{BE}} = - 1 \times \dfrac{2}{3}\]
Multiplying the terms, we get
\[ \Rightarrow \] \[{m_{BE}} = \dfrac{{ - 2}}{3}\]
Equation of the line CF is given with the point \[C(8,0)\] with slope \[\dfrac{2}{3}\]
So, using the formula \[y - {y_1} = m\left( {x - {x_1}} \right)\], we get
\[y - 0 = \dfrac{{ - 2}}{3}\left( {x - 8} \right)\]
\[ \Rightarrow \left( {y - 0} \right) = \dfrac{{ - 2}}{3}\left( {x - 8} \right)\]
\[ \Rightarrow y = \dfrac{{ - 2}}{3}x + \dfrac{{16}}{3}\] ………………………………………………………………………\[\left( 2 \right)\]
Now, we will find point of intersection of the lines AD and CF
Substituting equation\[\left( 1 \right)\]in equation \[\left( 2 \right)\], we get
\[\dfrac{2}{3}x = \dfrac{{ - 2}}{3}x + \dfrac{{16}}{3}\]

By rewriting the equation, we get
\[ \Rightarrow \dfrac{2}{3}x + \dfrac{2}{3}x = \dfrac{{16}}{3}\]
By cancelling the terms, we get
\[ \Rightarrow \dfrac{4}{3}x = \dfrac{{16}}{3}\]
\[ \Rightarrow x = \dfrac{{16}}{4}\]
Dividing 16 by 4, we get
\[ \Rightarrow x = 4\]
Substituting \[x = 4\] in equation \[\left( 1 \right)\], we get
\[y = \dfrac{2}{3}\left( x \right)\]
\[ \Rightarrow y = \dfrac{2}{3}\left( 4 \right)\]
Multiplying the terms, we get
\[ \Rightarrow y = \dfrac{8}{3}\]
Thus, the Point of Intersection is \[\left( {4,\dfrac{8}{3}} \right)\] .
Therefore, the orthocenter of the triangle formed by \[\left( {8,0} \right)\] and \[\left( {4,6} \right)\] with the origin is \[\left( {4,\dfrac{8}{3}} \right)\].

Note: We know that the orthocenter is defined as the point of intersection of the altitudes of a triangle. Altitudes of a triangle is a line drawn perpendicular from the vertex to the midpoint of the opposite to the vertex of a triangle. When three altitudes of a triangle meet at a point, then it is said to be the orthocenter. It is enough to find the slope of two sides and the equation of line for two altitudes, then we can find the orthocenter of a triangle which is the point of intersection of the two altitudes and not necessary to find the third altitude of a triangle.