Question

The orthocentre of a right angled triangle formed by (a,b), (a,c), (d,b) is :
(a) (a,b)
(b) (c,a)
(c) (b,d)
(d) (d,a)

Answer 1

Hint: To find the orthocentre, we need to find the equations of the lines perpendicular to each base and passing through the opposite vertex. We, then, have to simultaneously solve these three equations, to find the orthocentre of our triangle.

Complete step-by-step solution:
We know that an orthocentre is the point of intersection of all the three altitudes of a triangle.
In our problem, we have the three vertices of our triangle. Let these vertices be A (a,b), B (a,c) and C (d,b). Now, let us construct a figure using these three vertices.

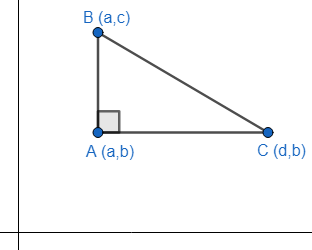
We know that the slope of a line passing through two points is $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.$
So, the slope of line BC is ${{m}_{BC}}=\dfrac{b-c}{d-a}.$
We know that the product of slopes of perpendicular lines is -1.
So, if D is a point on BC, such that, AD is the altitude on BC, then ${{m}_{AD}}\times {{m}_{BC}}=-1$
Hence, slope of AD, ${{m}_{AD}}=\dfrac{-1}{{{m}_{BC}}}$
$\Rightarrow {{m}_{AD}}=\dfrac{-1}{\left( \dfrac{b-c}{d-a} \right)}$
$\Rightarrow {{m}_{AD}}=\dfrac{a-d}{b-c}$
We can clearly see that A (a,b) is a point on AD.
We know that for a line of slope m passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ , the equation of the line is
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Therefore, the equation of the line AD is $y-b=\dfrac{a-d}{b-c}\left( x-a \right)...\left( i \right)$
Let E be a point on AC such that BE is the altitude on AC.
The slope of AC, \[{{m}_{AC}}=\dfrac{b-b}{d-a}=\dfrac{0}{d-a}=0\]
Here, we have, ${{m}_{BE}}\times {{m}_{AC}}=-1$
So, slope of BE, ${{m}_{BE}}=\dfrac{-1}{{{m}_{AC}}}$
$\Rightarrow {{m}_{BE}}=\dfrac{-1}{0}=\infty $
We know that a line with slope infinity is parallel to the y-axis. So, it will be of the form $x=k$ . But we know that B (a,c) is a point on this line. Thus, $a=k.$
So, the equation of line BE is, $x=a...\left( ii \right)$
Let F be a point on AB such that CF is the altitude on AB.
The slope of AB is, \[{{m}_{AB}}=\dfrac{c-b}{a-a}=\dfrac{c-b}{0}=\infty \]
Here, we have, ${{m}_{CF}}\times {{m}_{AB}}=-1$
So, slope of CF is, ${{m}_{CF}}=\dfrac{-1}{{{m}_{AB}}}$
$\Rightarrow {{m}_{CF}}=\dfrac{-1}{\infty }=0$
We know that a line with slope zero, is parallel to the x-axis. So, it will be of the form $y=l$ . But we know that C (d,b) is a point on this line. Thus, $b=l.$
So, the equation of CF is, $y=b...\left( iii \right)$
Now to find the orthocentre, we need to solve (i), (ii) and (iii) simultaneously.
Using just equation (ii) and (iii), we get $x=a\text{ and }y=b.$ Hence we have the point (a,b).
Putting $x=a\text{ and }y=b$ in equation (i), we get
$b-b=\dfrac{a-d}{b-c}\left( a-a \right)$
$\Rightarrow 0=0$
L.H.S. = R.H.S.
Thus, we see that (a,b) lies on equation (i).
Thus, the orthocentre is (a,b).
Hence, option (a) is the correct answer.

Note: We can clearly see that the altitude on AB is AC, and the altitude on AC is AB. Also, the intersection of AB and AC is A. Thus, the point A will be the orthocentre. We can also remember the fact that in a right-angled triangle, the orthocentre is the right-angled vertex.