
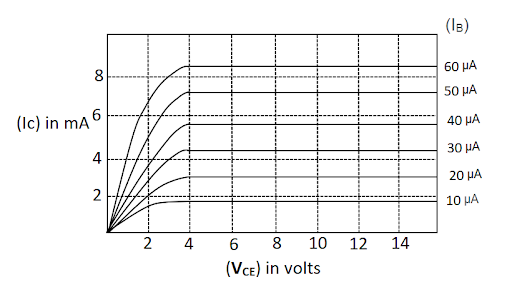
The output characteristics of a transistor is shown in the figure. When \[{V_{CE}}\] is 10V and \[{I_C}\]= 4.0 mA, then the value of \[{\beta _{ac}}\] is __________.
Answer
135k+ views
Hint:A transistor is defined as a semiconductor device used to conduct an electric current or electric voltage. For a transistor, the three terminals are base, collector and emitter. When we combine the expressions for \[\alpha \] and \[\beta \] the mathematical relationship between these parameters then we get the current gain of the transistor. By using the relation, we can find the value for \[\beta \].
Formula used:
The mathematical relationship between these parameters can be given as:
\[\alpha = \dfrac{{{I_C}}}{{{I_E}}}\] and \[\beta = \dfrac{{{I_C}}}{{{I_B}}}\]
\[\Rightarrow {I_C} = \alpha {I_E} = \beta {I_B}\]
As \[\alpha = \dfrac{\beta }{{\beta + 1}}\]
\[\beta = \dfrac{\alpha }{{1 - \alpha }}\]
\[{I_E} = {I_C} + {I_B}\]
Where \[{I_C}\] is the current in the collector terminal, \[{I_B}\] is the current in the base terminal and \[{I_E}\] is the current in the emitter terminal.
Complete step by step solution:
A transistor can also use a small signal which is applied between one pair of its terminals to control a large signal at the other pair of terminals. This property is known as gain. A stronger output signal can produce a voltage as well as a current which is dependable on a weaker input signal.
\[\beta = \dfrac{{\Delta {I_c}}}{{\Delta {I_B}}}\]
Substituting the values
\[\Delta {I_B} = 30 - 20{I_C} = 4\,mA\]
\[\Rightarrow \Delta {I_C} = 4.5 - 3 = 1.5\,mA\]
Now \[\beta = \dfrac{{1.5 \times {{10}^{ - 3}}}}{{10 \times {{10}^{ - 6}}}}\]
\[\therefore \beta = 150\]
Therefore, the value of \[{\beta _{ac}}\] is 150.
Note: In physics, for any transistor the graph shows the relationships between the current(I) and the voltage (V) for any configuration is known as transistor characteristics. The current transfer properties curve can define the variation of output current to the input current by keeping the output voltage constant. There are three transistor circuit configurations. These are Common Emitter Transistor, Common Base Transistor and Common Collector Transistor.
Formula used:
The mathematical relationship between these parameters can be given as:
\[\alpha = \dfrac{{{I_C}}}{{{I_E}}}\] and \[\beta = \dfrac{{{I_C}}}{{{I_B}}}\]
\[\Rightarrow {I_C} = \alpha {I_E} = \beta {I_B}\]
As \[\alpha = \dfrac{\beta }{{\beta + 1}}\]
\[\beta = \dfrac{\alpha }{{1 - \alpha }}\]
\[{I_E} = {I_C} + {I_B}\]
Where \[{I_C}\] is the current in the collector terminal, \[{I_B}\] is the current in the base terminal and \[{I_E}\] is the current in the emitter terminal.
Complete step by step solution:
A transistor can also use a small signal which is applied between one pair of its terminals to control a large signal at the other pair of terminals. This property is known as gain. A stronger output signal can produce a voltage as well as a current which is dependable on a weaker input signal.
\[\beta = \dfrac{{\Delta {I_c}}}{{\Delta {I_B}}}\]
Substituting the values
\[\Delta {I_B} = 30 - 20{I_C} = 4\,mA\]
\[\Rightarrow \Delta {I_C} = 4.5 - 3 = 1.5\,mA\]
Now \[\beta = \dfrac{{1.5 \times {{10}^{ - 3}}}}{{10 \times {{10}^{ - 6}}}}\]
\[\therefore \beta = 150\]
Therefore, the value of \[{\beta _{ac}}\] is 150.
Note: In physics, for any transistor the graph shows the relationships between the current(I) and the voltage (V) for any configuration is known as transistor characteristics. The current transfer properties curve can define the variation of output current to the input current by keeping the output voltage constant. There are three transistor circuit configurations. These are Common Emitter Transistor, Common Base Transistor and Common Collector Transistor.
Recently Updated Pages
JEE Main 2021 July 25 Shift 2 Question Paper with Answer Key

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 20 Shift 2 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

How to find Oxidation Number - Important Concepts for JEE

Half-Life of Order Reactions - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Elastic Collisions in One Dimension - JEE Important Topic

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Displacement-Time Graph and Velocity-Time Graph for JEE

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

JEE Advanced 2024 Syllabus Weightage

JEE Main Chemistry Question Paper with Answer Keys and Solutions




