Answer
Verified445.5k+ views
Hint: We draw a diagram of the trapezium and calculate the height of the trapezium using Pythagoras theorem in a triangle formed with one of the non-parallel sides. Use the formula of the area of trapezium to calculate the area.
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse. In the right triangle the largest side opposite to the right angle is the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]
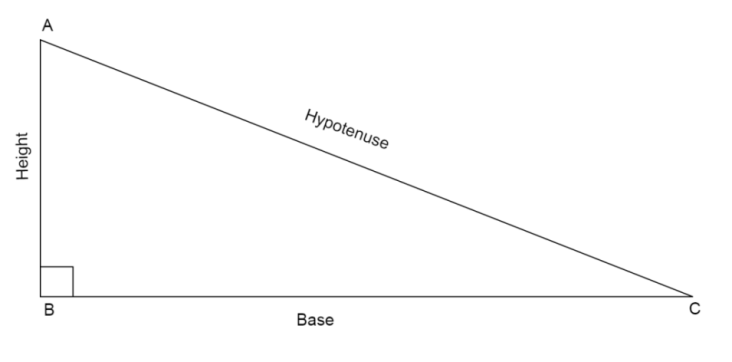
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]
* Trapezium: A quadrilateral having one pair of opposite sides parallel is called a trapezium
* Area of trapezium having parallel sides ‘a’ and ‘b’ with height ‘h’ is given by \[\dfrac{{a + b}}{2} \times h\]
Step-By-Step answer:
We draw the diagram of the trapezium with given dimensions.
Parallel sides have lengths 20cm and 32cm.
Non parallel sides are equal in length as 10cm.
Draw a line representing height of the trapezium.
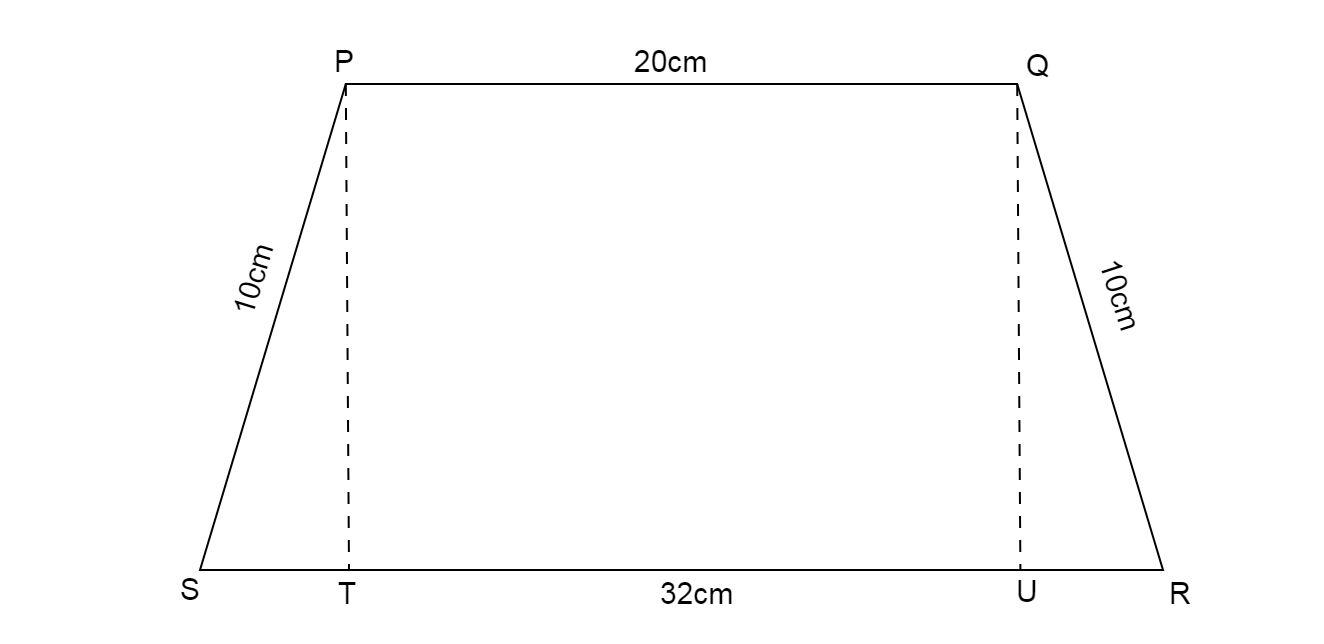
We have PQRS as a trapezium.
We draw altitudes from P and Q to the side SR.
Since PT and QU are altitudes, then the side TU becomes equal in length to side PQ
\[ \Rightarrow PQ = TU = 20\]cm
Also, the altitudes are equal in length, let us take \[PT = TU = x\]
Now in triangles PST and QUR, since pairs of two sides are equal in lengths then it is confirmed that the length of the third side will also be equal.
\[ \Rightarrow ST = UR = y\](Say)
Now we calculate the length of ST.
We know \[SR = 32\]cm
Break the side SR in three parts i.e. \[SR = ST + TU + UR\]
\[ \Rightarrow ST + TU + UR = 32\]
Substitute the value of \[ST = UR = y;TU = 20\] in RHS
\[ \Rightarrow y + 20 + y = 32\]
\[ \Rightarrow 2y + 20 = 32\]
Cancel 2 from both sides of the equation
\[ \Rightarrow y + 10 = 16\]
Shift all constants to RHS
\[ \Rightarrow y = 16 - 10\]
\[ \Rightarrow y = 6\]
So, the length of side \[ST = 6\]cm
Now since \[\vartriangle PST\] is a right triangle, we can apply Pythagoras theorem
\[ \Rightarrow P{S^2} = P{T^2} + S{T^2}\]
Substitute the values of \[PS = 10,ST = 6,PT = x\]
\[ \Rightarrow {(10)^2} = {x^2} + {(6)^2}\]
\[ \Rightarrow 100 = {x^2} + 36\]
Shift all constant values to one side
\[ \Rightarrow 100 - 36 = {x^2}\]
\[ \Rightarrow {x^2} = 64\]
We can write \[64 = {(8)^2}\]
\[ \Rightarrow {x^2} = {(8)^2}\]
Take under root on both sides of the equation
\[ \Rightarrow \sqrt {{x^2}} = \sqrt {{{(8)}^2}} \]
Cancel square root by square power on both sides
\[ \Rightarrow x = 8\]
So, the height of the trapezium is 8cm
Now we calculate the area of trapezium PQRS
Since we know area of trapezium having parallel sides ‘a’ and ‘b’ with height ‘h’ is given by \[\dfrac{{a + b}}{2} \times h\]
Here value of \[a = 20,b = 32,h = 8\]
\[ \Rightarrow \]Area of PQRS \[ = \left( {\dfrac{{20 + 32}}{2} \times 8} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of PQRS \[ = \left( {\dfrac{{52}}{2} \times 8} \right)\]\[c{m^2}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of PQRS \[ = \left( {26 \times 8} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of PQRS \[ = 208\]\[c{m^2}\]
\[\therefore \]Option C is correct.
Note: Many students make the mistake of assuming the quadrilateral formed inside with altitudes and parallel sides as a square which is wrong, keep in mind we are not given that the altitude forms a square. Students are likely to make mistakes while applying Pythagoras theorem as many students write any side on any side of the equation, keep in mind the hypotenuse (largest side) is on one side of the equation and base and perpendicular are on the other side of the equation.
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse. In the right triangle the largest side opposite to the right angle is the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]
* Trapezium: A quadrilateral having one pair of opposite sides parallel is called a trapezium
* Area of trapezium having parallel sides ‘a’ and ‘b’ with height ‘h’ is given by \[\dfrac{{a + b}}{2} \times h\]
Step-By-Step answer:
We draw the diagram of the trapezium with given dimensions.
Parallel sides have lengths 20cm and 32cm.
Non parallel sides are equal in length as 10cm.
Draw a line representing height of the trapezium.
We have PQRS as a trapezium.
We draw altitudes from P and Q to the side SR.
Since PT and QU are altitudes, then the side TU becomes equal in length to side PQ
\[ \Rightarrow PQ = TU = 20\]cm
Also, the altitudes are equal in length, let us take \[PT = TU = x\]
Now in triangles PST and QUR, since pairs of two sides are equal in lengths then it is confirmed that the length of the third side will also be equal.
\[ \Rightarrow ST = UR = y\](Say)
Now we calculate the length of ST.
We know \[SR = 32\]cm
Break the side SR in three parts i.e. \[SR = ST + TU + UR\]
\[ \Rightarrow ST + TU + UR = 32\]
Substitute the value of \[ST = UR = y;TU = 20\] in RHS
\[ \Rightarrow y + 20 + y = 32\]
\[ \Rightarrow 2y + 20 = 32\]
Cancel 2 from both sides of the equation
\[ \Rightarrow y + 10 = 16\]
Shift all constants to RHS
\[ \Rightarrow y = 16 - 10\]
\[ \Rightarrow y = 6\]
So, the length of side \[ST = 6\]cm
Now since \[\vartriangle PST\] is a right triangle, we can apply Pythagoras theorem
\[ \Rightarrow P{S^2} = P{T^2} + S{T^2}\]
Substitute the values of \[PS = 10,ST = 6,PT = x\]
\[ \Rightarrow {(10)^2} = {x^2} + {(6)^2}\]
\[ \Rightarrow 100 = {x^2} + 36\]
Shift all constant values to one side
\[ \Rightarrow 100 - 36 = {x^2}\]
\[ \Rightarrow {x^2} = 64\]
We can write \[64 = {(8)^2}\]
\[ \Rightarrow {x^2} = {(8)^2}\]
Take under root on both sides of the equation
\[ \Rightarrow \sqrt {{x^2}} = \sqrt {{{(8)}^2}} \]
Cancel square root by square power on both sides
\[ \Rightarrow x = 8\]
So, the height of the trapezium is 8cm
Now we calculate the area of trapezium PQRS
Since we know area of trapezium having parallel sides ‘a’ and ‘b’ with height ‘h’ is given by \[\dfrac{{a + b}}{2} \times h\]
Here value of \[a = 20,b = 32,h = 8\]
\[ \Rightarrow \]Area of PQRS \[ = \left( {\dfrac{{20 + 32}}{2} \times 8} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of PQRS \[ = \left( {\dfrac{{52}}{2} \times 8} \right)\]\[c{m^2}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of PQRS \[ = \left( {26 \times 8} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of PQRS \[ = 208\]\[c{m^2}\]
\[\therefore \]Option C is correct.
Note: Many students make the mistake of assuming the quadrilateral formed inside with altitudes and parallel sides as a square which is wrong, keep in mind we are not given that the altitude forms a square. Students are likely to make mistakes while applying Pythagoras theorem as many students write any side on any side of the equation, keep in mind the hypotenuse (largest side) is on one side of the equation and base and perpendicular are on the other side of the equation.