Question

The parallel sides of trapezium are 20cm and 10cm. Its non-parallel sides are 13cm each. Find the area of trapezium?
(A)$120c{m^2}$
(B) $180c{m^2}$
(C) $210c{m^2}$
(D) $150c{m^2}$

Answer 1

Hint: In this type of question we can solve this with the help of the diagram in which as there is a perpendicular in on base so it makes the diagram in three section in which 2 are the triangles and 1 is rectangle so we can solves with adding the formula of the Areas of triangles and area of rectangle.

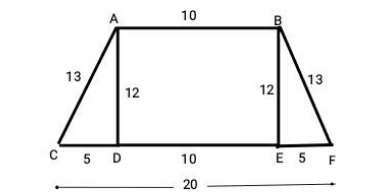
Complete step-by-step answer:
As we know we have given sides 20cm and 10cm and a perpendicular is 13cm.
Now with the help of diagram we can see here two perpendiculars form triangles i.e. $\Delta ACD$ and $\Delta BEF.$
We will find out the value of the distance AD which will help in finding the area of rectangle
First we will find values of AD and BE by Pythagoras theorem
First we find the value of AD, we get
 \[ \Rightarrow AD = \sqrt {{{\left( {AC} \right)}^2} - {{\left( {CD} \right)}^2}} \]
Now we put the value of AC and CD from the figure, we get
$ \Rightarrow AD = \sqrt {{{\left( {13} \right)}^2} - {{\left( 5 \right)}^2}} $
By solving the squares we get
$ \Rightarrow AD = \sqrt {169 - 25} $
By subtracting we get,
 $ \Rightarrow AD = \sqrt {144} $
Now by finding the square root of the above number we get
\[ \Rightarrow AD{\text{ }} = {\text{ }}12cm\]
Now we will calculate value of BE
\[ \Rightarrow BE = \sqrt {B{F^2} - E{F^2}} \]
Now we put the value of BF and EF from the figure, we get
$ \Rightarrow BE = \sqrt {{{\left( {13} \right)}^2} - {{\left( 5 \right)}^2}} $
By solving the squares we get
$ \Rightarrow BE = \sqrt {169 - 25} $
By subtracting we get,
 $ \Rightarrow BE = \sqrt {144} $
Now by finding the square root of the above number we get
\[ \Rightarrow BE{\text{ }} = {\text{ }}12cm\]
Now we will use the formulas of area of rectangle and areas of triangles for finding our answer which is area of trapezium.
Area of trapezium = Area of rectangle ABDE + area of triangle ACD + area of triangle BEF
Area of trapezium = $\left[ {\left( {length \times breadth} \right) + \left( {\dfrac{1}{2} \times base \times length} \right) + \left( {\dfrac{1}{2} \times base \times length} \right)} \right]$
Now we out the values in the formula, we get
Area of trapezium = $\left[ {\left( {12 \times 10} \right) + \left( {\dfrac{1}{2} \times 5 \times 12} \right) + \left( {\dfrac{1}{2} \times 5 \times 12} \right)} \right]$
Now we solve the equation, we get
Area of trapezium = $\left[ {120 + 30 + 30} \right]$
After adding the terms we get,
Area of trapezium = $180c{m^2}$
Therefor area of trapezium is $180c{m^2}$

Hence option B is correct.

Note: In this type of question we can use the direct formula of Area of trapezium and we can find out the answer and the area of trapezium which is - $\dfrac{{\text{1}}}{{\text{2}}}{{ \times {\text{height}} \times }}\left( {{\text{sum of the parallel sides}}} \right)$.