Question

The perimeter of a school volleyball court is 177ft and the length is twice the width. What are the dimensions of the volleyball court?

Answer 1

Hint: We know the perimeter of a rectangular school volleyball court is \[P=2\left( l+w \right)\] where “P” is the perimeter, “l” is the length and “w” is the width of the school volleyball court. First assume the value of width and with that find the value of length. Perimeter is given. Put all the values in the formulae and after evaluating it we can get the answer easily.

Complete step-by-step answer:
According to the question the perimeter of a school volleyball court is 177ft.
Let us assume that the width of the volleyball field is
\[w=b\]
From the question we know that length is twice the width. So the length is
\[l=2b\]
Now let us imagine the volleyball field layout by the diagram below.

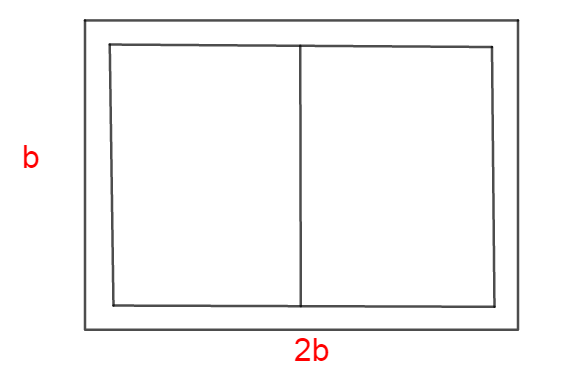
We know the formula of perimeter of a rectangular field is
\[P=2\left( l+w \right)\]
From the question we know the perimeter of a school volleyball court is 177ft.
Now replacing the value of “P” with the value 177 we get,
\[177=2\left( l+w \right)\]
Now put the assumed value of length and width of school volleyball court we get,

\[\begin{align}
  & 177=2\left( 2b+b \right) \\
 & \Rightarrow 177=2\times 3b \\
 & \Rightarrow 6b=177 \\
 & \Rightarrow b=\dfrac{177}{6} \\
 & \Rightarrow b=29.5 \\
\end{align}\]

So the width of the school volleyball court is 29.5ft.
We know that length is twice the width.
The length of the school volleyball court is
\[\begin{align}
  & 2\times b \\
 & \Rightarrow 29.5\times 2 \\
 & \Rightarrow 59 \\
\end{align}\]

The length and the width of the school volleyball court is 59ft and 29.5ft respectively.

Note: We can assume the value of length \[l\]. the value of width will be \[\dfrac{l}{2}\].
Perimeter is given 177ft. putting all the values in the formulae we get
\[\begin{align}
  & P=2\left( l+w \right) \\
 & \Rightarrow 177=2\left( l+\dfrac{l}{2} \right) \\
 & \Rightarrow 177=2\times \left( \dfrac{2l+l}{2} \right) \\
 & \Rightarrow 3l=177 \\
 & \Rightarrow l=\dfrac{177}{3} \\
 & \Rightarrow l=59 \\
\end{align}\]

Length is 59ft. Width is
\[\begin{align}
  & w=\dfrac{l}{2} \\
 & \Rightarrow w=\dfrac{59}{2} \\
 & \Rightarrow w=29.5 \\
\end{align}\]

The length and the width of the school volleyball court is 59ft and 29.5ft respectively.