
The potential difference across $ 8 $ ohm resistance is $ 48 $ volt as shown in the figure. The value of potential difference across X and Y points will be
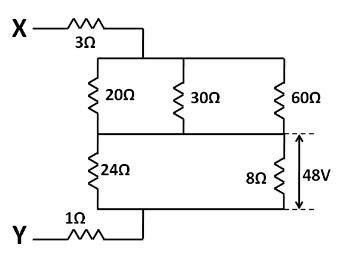
(A) $ 128 $ volt
(B) $ 160 $ volt
(C) $ 80 $ volt
(D) $ 62 $ volt

Answer
459.3k+ views
Hint : To solve this question, we need to assume a battery between the points X and Y of emf equal to the unknown potential difference. Then we have to simplify the circuit by calculating the parallel equivalent resistance.
Complete step by step answer
Let the potential difference across X and Y points be $ V $ . So let us consider a battery of emf $ V $ connected across the points X and Y as shown in the figure below.
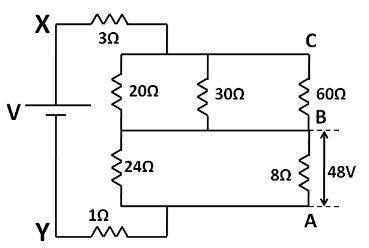
According to the question, the potential difference across the $ 8 $ ohm resistance is equal to $ 48 $ volt. So referring to the above figure, the potential difference between the points A and B is $ 48 $ volt. According to the polarity of the battery, the point B should be at a higher potential than the point A. So we have
$\Rightarrow {V_{BA}} = 8{\text{V}} $ ……………………….(1)
Now, the $ 24\Omega $ and $ 8\Omega $ resistances are in parallel combination across the point A and B. So the equivalent resistance between the points A and B, $ {R_{AB}} $ is given by
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{8} + \dfrac{1}{{24}} $
On solving we get
$\Rightarrow {R_{AB}} = 6\Omega $
Also, across the points B and C, the $ 20\Omega ,30\Omega ,60\Omega $ resistances are arranged in parallel combination. So the equivalent resistance across the points B and C is given by
$\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{60}} $
On solving we get
$\Rightarrow {R_{BC}} = 10\Omega $
So the above circuit can be redrawn as
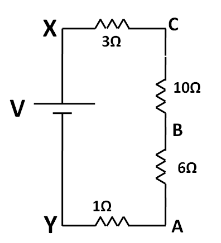
Now, let $ I $ be the current in the circuit. From Ohm’s law we have
$\Rightarrow V = IR $ ..........................(2)
Now, the equivalent resistance in the circuit is given by
$\Rightarrow R = 3\Omega + 10\Omega + 6\Omega + 1\Omega $
$ \Rightarrow R = 20\Omega $
So from (2) we have
$\Rightarrow V = 20I $
$ \Rightarrow I = \dfrac{V}{{20}} $ ........................(3)
The potential difference across the points A and B is equal to that across the $ 6\Omega $ resistance. Therefore we have
$\Rightarrow {V_{BA}} = 6I $
From (3)
$\Rightarrow {V_{BA}} = \dfrac{{6V}}{{20}} $ ........................(4)
Equating (1) and (4) we have
$\Rightarrow \dfrac{{6V}}{{20}} = 48 $
$ \Rightarrow V = 160{\text{V}} $
Thus, the potential difference between the points X and Y is equal to $ 160 $ volts.
Hence, the correct answer is option B.
Note
The points X and Y are not shown to be connected through any battery in the figure given in the question. But the potential difference which is given across the $ 8 $ ohm resistance clearly indicates that a voltage source must be present there. Hence we were able to assume the battery between X and Y.
Complete step by step answer
Let the potential difference across X and Y points be $ V $ . So let us consider a battery of emf $ V $ connected across the points X and Y as shown in the figure below.

According to the question, the potential difference across the $ 8 $ ohm resistance is equal to $ 48 $ volt. So referring to the above figure, the potential difference between the points A and B is $ 48 $ volt. According to the polarity of the battery, the point B should be at a higher potential than the point A. So we have
$\Rightarrow {V_{BA}} = 8{\text{V}} $ ……………………….(1)
Now, the $ 24\Omega $ and $ 8\Omega $ resistances are in parallel combination across the point A and B. So the equivalent resistance between the points A and B, $ {R_{AB}} $ is given by
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{8} + \dfrac{1}{{24}} $
On solving we get
$\Rightarrow {R_{AB}} = 6\Omega $
Also, across the points B and C, the $ 20\Omega ,30\Omega ,60\Omega $ resistances are arranged in parallel combination. So the equivalent resistance across the points B and C is given by
$\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{60}} $
On solving we get
$\Rightarrow {R_{BC}} = 10\Omega $
So the above circuit can be redrawn as

Now, let $ I $ be the current in the circuit. From Ohm’s law we have
$\Rightarrow V = IR $ ..........................(2)
Now, the equivalent resistance in the circuit is given by
$\Rightarrow R = 3\Omega + 10\Omega + 6\Omega + 1\Omega $
$ \Rightarrow R = 20\Omega $
So from (2) we have
$\Rightarrow V = 20I $
$ \Rightarrow I = \dfrac{V}{{20}} $ ........................(3)
The potential difference across the points A and B is equal to that across the $ 6\Omega $ resistance. Therefore we have
$\Rightarrow {V_{BA}} = 6I $
From (3)
$\Rightarrow {V_{BA}} = \dfrac{{6V}}{{20}} $ ........................(4)
Equating (1) and (4) we have
$\Rightarrow \dfrac{{6V}}{{20}} = 48 $
$ \Rightarrow V = 160{\text{V}} $
Thus, the potential difference between the points X and Y is equal to $ 160 $ volts.
Hence, the correct answer is option B.
Note
The points X and Y are not shown to be connected through any battery in the figure given in the question. But the potential difference which is given across the $ 8 $ ohm resistance clearly indicates that a voltage source must be present there. Hence we were able to assume the battery between X and Y.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

What is a transformer Explain the principle construction class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE




