
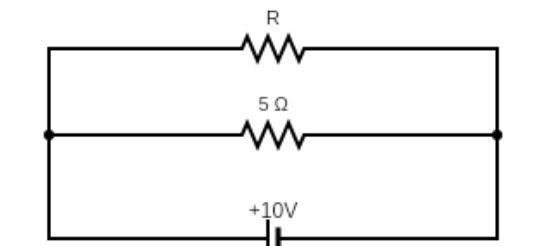
The power dissipated in the circuit shown in the figure is 30 watts. The value of \[R\] is
(A) \[15\Omega \]
(B) \[10\Omega \]
(C) \[30\Omega \]
(D) \[20\Omega \]
Answer
125.7k+ views
Hint: The voltage across resistors in parallel is the same. The total power consumed is the sum of the power consumed by the individual resistor
Formula used: In this solution we will be using the following formulae;
\[P = \dfrac{{{V^2}}}{R}\] where \[P\] is the power consumed in a circuit, \[V\]is the voltage connected to the circuit, \[R\] is the effective or equivalent resistance in the circuit.
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_{eq}}\] is the equivalent resistance of two resistors, and \[{R_1}\] and \[{R_2}\] are the individual resistances of the resistor.
Complete Step-by-Step Solution:
We are given the total power consumed in the circuit, and asked to find the resistance \[R\].
We see that the resistance \[R\] is connected in parallel to the resistance \[5\Omega \]. Hence, the voltage across both of them are equal. And the voltage is equal to 10 V.
The total power consumed in the circuit can be given as
\[P = \dfrac{{{V^2}}}{R}\] where \[P\] is the power consumed in a circuit, \[V\]is the voltage connected to the circuit, \[R\] is the effective or equivalent resistance in the circuit.
We find the equivalent resistance in the circuit.
Equivalent resistance of a circuit can be given as
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_1}\] and \[{R_2}\] are the individual resistances of the resistor.
Hence,
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{5}\]
\[ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{5 + R}}{{5R}}\]
Hence, inverting it, we get
\[{R_{eq}} = \dfrac{{5R}}{{5 + R}}\]
Hence, the power is given as
\[P = \dfrac{{{V^2}}}{{\dfrac{{5R}}{{5 + R}}}}\]
Hence,
\[30 = \dfrac{{{{10}^2}}}{{\dfrac{{5R}}{{5 + R}}}} = \dfrac{{100(5 + R)}}{{5R}}\]
Dividing both sides by 10, and cross multiplying, we have
\[3R = 10 + 2R\]
\[R = 10\Omega \]
Hence, the correct option is B.
Note: Alternatively, the total power consumed in the circuit is the sum of the power consumed in the individual resistance, hence, we can write that
\[P = \dfrac{{{V^2}}}{{{R_5}}} + \dfrac{{{V^2}}}{R}\] where \[{R_5}\] is the 5 ohms resistance.
If we factorize out \[{V^2}\]and put the value of the 5 ohms we have
\[P = {V^2}\left( {\dfrac{1}{5} + \dfrac{1}{R}} \right)\]
\[P = {V^2}\left( {\dfrac{{5 + R}}{{5R}}} \right)\] which can be written as
\[P = \dfrac{{{V^2}}}{{\dfrac{{5R}}{{5 + R}}}}\] which is identical to the formula in the solution.
Formula used: In this solution we will be using the following formulae;
\[P = \dfrac{{{V^2}}}{R}\] where \[P\] is the power consumed in a circuit, \[V\]is the voltage connected to the circuit, \[R\] is the effective or equivalent resistance in the circuit.
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_{eq}}\] is the equivalent resistance of two resistors, and \[{R_1}\] and \[{R_2}\] are the individual resistances of the resistor.
Complete Step-by-Step Solution:
We are given the total power consumed in the circuit, and asked to find the resistance \[R\].
We see that the resistance \[R\] is connected in parallel to the resistance \[5\Omega \]. Hence, the voltage across both of them are equal. And the voltage is equal to 10 V.
The total power consumed in the circuit can be given as
\[P = \dfrac{{{V^2}}}{R}\] where \[P\] is the power consumed in a circuit, \[V\]is the voltage connected to the circuit, \[R\] is the effective or equivalent resistance in the circuit.
We find the equivalent resistance in the circuit.
Equivalent resistance of a circuit can be given as
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_1}\] and \[{R_2}\] are the individual resistances of the resistor.
Hence,
\[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{R} + \dfrac{1}{5}\]
\[ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{5 + R}}{{5R}}\]
Hence, inverting it, we get
\[{R_{eq}} = \dfrac{{5R}}{{5 + R}}\]
Hence, the power is given as
\[P = \dfrac{{{V^2}}}{{\dfrac{{5R}}{{5 + R}}}}\]
Hence,
\[30 = \dfrac{{{{10}^2}}}{{\dfrac{{5R}}{{5 + R}}}} = \dfrac{{100(5 + R)}}{{5R}}\]
Dividing both sides by 10, and cross multiplying, we have
\[3R = 10 + 2R\]
\[R = 10\Omega \]
Hence, the correct option is B.
Note: Alternatively, the total power consumed in the circuit is the sum of the power consumed in the individual resistance, hence, we can write that
\[P = \dfrac{{{V^2}}}{{{R_5}}} + \dfrac{{{V^2}}}{R}\] where \[{R_5}\] is the 5 ohms resistance.
If we factorize out \[{V^2}\]and put the value of the 5 ohms we have
\[P = {V^2}\left( {\dfrac{1}{5} + \dfrac{1}{R}} \right)\]
\[P = {V^2}\left( {\dfrac{{5 + R}}{{5R}}} \right)\] which can be written as
\[P = \dfrac{{{V^2}}}{{\dfrac{{5R}}{{5 + R}}}}\] which is identical to the formula in the solution.
Recently Updated Pages
Wheatstone Bridge - Working Principle, Formula, Derivation, Application

Young's Double Slit Experiment Step by Step Derivation

JEE Main 2023 (April 8th Shift 2) Physics Question Paper with Answer Key

JEE Main 2023 (January 30th Shift 2) Maths Question Paper with Answer Key

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

Classification of Elements and Periodicity in Properties Chapter For JEE Main Chemistry

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

The formula of the kinetic mass of a photon is Where class 12 physics JEE_Main

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Main Login 2045: Step-by-Step Instructions and Details

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!

JEE Main 2025: Derivation of Equation of Trajectory in Physics




