
The quadratic polynomial having zeros are 1 and -2 is.
(a)
(b)
(c)
(d)
Answer
518.4k+ views
1 likes
Hint: For solving this question we will simply find the sum and the product of the given roots and substitute their values in the formula
Complete step-by-step solution -
Given:
We have to find the quadratic polynomial having roots 1 and -2.
Now, before we proceed we should know that if
Now, we come back to our question in which we have to find the quadratic polynomial having roots 1 and 2. And from the above discussion, we can say that the required polynomial will be
Now, from the above result, we conclude that the quadratic polynomial having zeros 1 and -2 will be
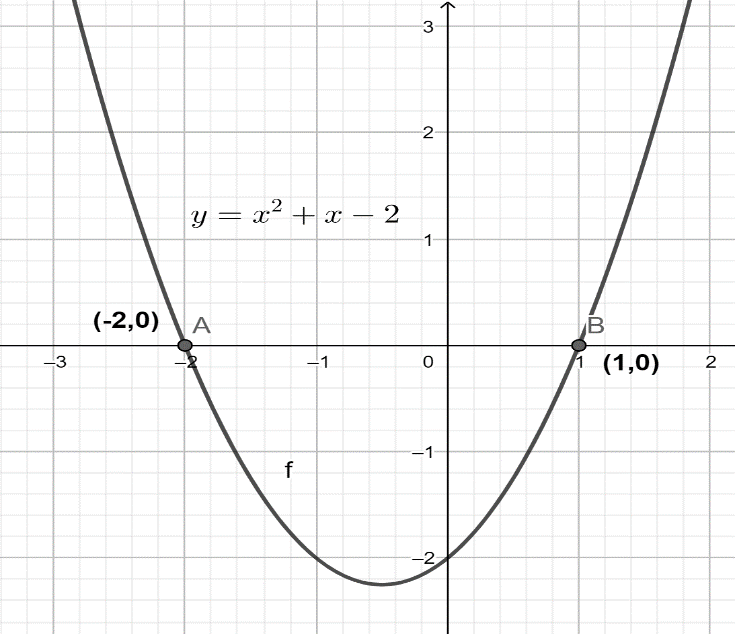
In the above figure, the curve
Thus,
Hence, option (c) will be the correct option.
Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the problem is very easy, but we should write the expression of the required polynomial without any mistake and in the end, we should verify our answer with a graph and strengthen our basic concepts.
Complete step-by-step solution -
Given:
We have to find the quadratic polynomial having roots 1 and -2.
Now, before we proceed we should know that if
Now, we come back to our question in which we have to find the quadratic polynomial having roots 1 and 2. And from the above discussion, we can say that the required polynomial will be
Now, from the above result, we conclude that the quadratic polynomial having zeros 1 and -2 will be

In the above figure, the curve
Thus,
Hence, option (c) will be the correct option.
Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the problem is very easy, but we should write the expression of the required polynomial without any mistake and in the end, we should verify our answer with a graph and strengthen our basic concepts.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE




