Question

The quadrilateral in which only opposite side is parallel is called
$\begin{align}
  & \text{a) square} \\
 & \text{b) rectangle} \\
 & \text{c) Rhombus} \\
 & \text{d) Trapezium}\text{. } \\
\end{align}$

Answer 1

Hint: Now we know that a quadrilateral is any closed geometrical figure with 4 sides. Now each quadrilateral has its own properties. We will check for the quadrilateral which has opposite sides parallel.

Complete step-by-step solution:
Now first let us understand what a quadrilateral is: a closed figure which has 4 sides.
Hence quadrilateral is nothing but a polygon with 4 points.
Now there are some general shapes of a quadrilateral, for example, square, rectangle, parallelogram, etc.
Now let us first see some of the properties of each quadrilateral.
Let us first check the properties of Square.
A square is a quadrilateral with all the sides the same and all the angles equal to ${{90}^{\circ }}$.
Also, the opposite angles of the square are parallel.

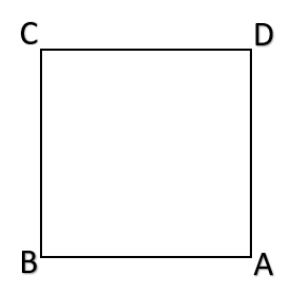
Now here AB = BC = CD = AD, $\angle A=\angle B=\angle C=\angle D={{90}^{\circ }}$
Also, we have AB is parallel to CD and BC is parallel to AD.
Now let us consider the quadrilateral rectangle.
The rectangle is a quadrilateral with opposite sides equal and parallel and all angles equal to ${{90}^{\circ }}$
Hence a rectangle looks like,

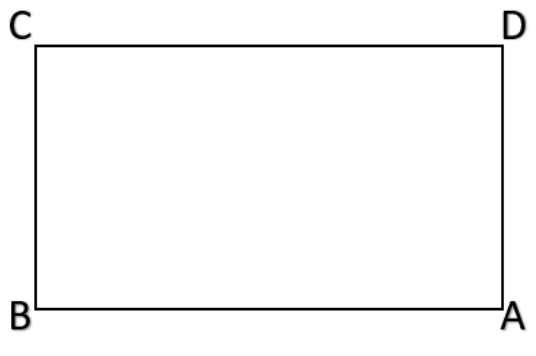
Here AB is parallel to CD and AB = CD also BC is parallel to AD and BC = AD.
Also $\angle A=\angle B=\angle C=\angle D={{90}^{\circ }}$ .
Now consider the quadrilateral Rhombus.
Rhombus is a quadrilateral where each pair of opposite sides are parallel and all the length of sides are equal.
Hence if we draw a rhombus it looks like.

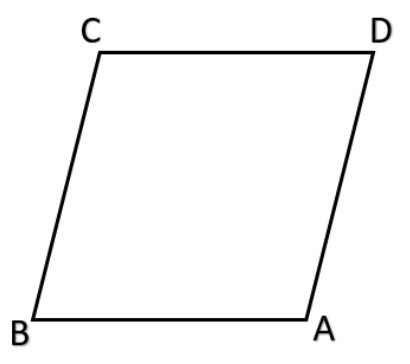
Now note that here AB is parallel to CD and BC is parallel to AD also AB = BC = CD = AD.
Now let us understand the quadrilateral trapezium.
The trapezium is a quadrilateral with one pair of opposite sides parallel. There is no other restriction on other sides and angles.
Let us check the figure of the trapezium.

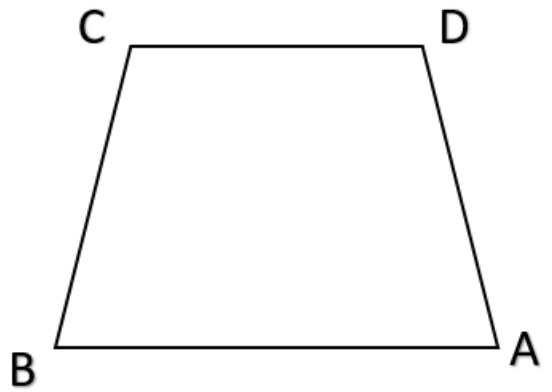
Here note that AB is parallel to CD.
Hence we have the quadrilateral with only one pair of opposite sides parallel is a trapezium. Option d is the correct option.

Note: Now note that a square satisfies all the properties of the Rhombus and hence a square is always a rhombus. But a rhombus is not always a square as the additional condition of the angels comes in. Similarly, we have every square is a rectangle by every rectangle is not a square.