
The radius of the largest sphere which fits properly at the center of the edge of body centered cubic unit cell is: (edge length is represented by a)
(A) 0.134a
(B) 0.027a
(C) 0.067a
(D) 0.047a
Answer
466.2k+ views
Hint: A unit cell is the smallest repeating unit in the crystal lattice, it is the building block of a crystal like the cell which is the building block of the human body. Body centered cubic cell is one of the types of the unit cell.
Complete step by step solution:
To solve this question we have to find the relation between the radius (r) and the edge of the body centered unit cell (a). We know that the total number of atoms present in the body centered cubic cell is = 2.
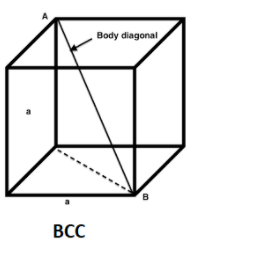
In body centered unit cells, atoms in the body diagonals are in contact with each other. So the length of the body diagonal is =
The body diagonal =
So, 4R =
According to the question
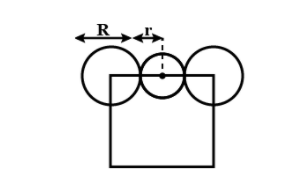
From equation 1 and 2
r = 0.067a
Hence the correct answer is option (C)
Note: In the body centered unit cell, atoms are present at the center and at the corner of the cube. And as we know that there is only one center in a cube hence only one atom is completely present there that means that this atom is not shared with any other unit cell and one atom at the corner contributes to eight other corners. So the total number of atoms present in the body centered cubic cell is = 2. i.e.
1 atom at body center
Complete step by step solution:
To solve this question we have to find the relation between the radius (r) and the edge of the body centered unit cell (a). We know that the total number of atoms present in the body centered cubic cell is = 2.

In body centered unit cells, atoms in the body diagonals are in contact with each other. So the length of the body diagonal is =
The body diagonal =
So, 4R =
According to the question

From equation 1 and 2
r = 0.067a
Hence the correct answer is option (C)
Note: In the body centered unit cell, atoms are present at the center and at the corner of the cube. And as we know that there is only one center in a cube hence only one atom is completely present there that means that this atom is not shared with any other unit cell and one atom at the corner contributes to eight other corners. So the total number of atoms present in the body centered cubic cell is = 2. i.e.
1 atom at body center
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
The probability that a leap year will have only 52 class 12 maths CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

The final image formed by a compound microscope is class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What are the major means of transport Explain each class 12 social science CBSE

Which of the following properties of a proton can change class 12 physics CBSE




