Question

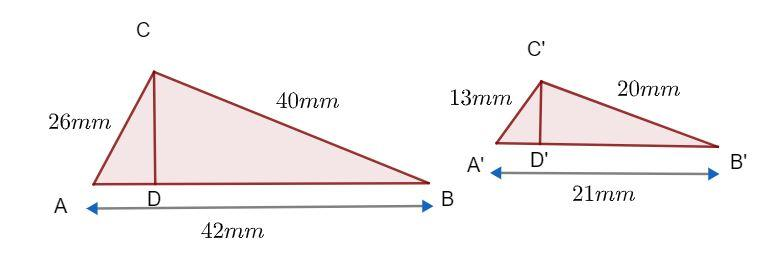
The ratio of the corresponding sides of similar triangles $ABC$ and \[A'B'C'\] is $2:1$ . Also, the altitudes $CD$ and $C'D'$ , that we have drawn in these triangles are also in the same ratio $2:1$ . Then, prove that the ratio of their areas is equal to the square of the ratio of their corresponding sides.

Answer 1

Hint: We need to prove that the ratio of areas of $ABC$ and \[A'B'C'\] is equal to the square of the ratio of their corresponding sides. First we will show, using similarity properties of triangles, that the ratio of corresponding medians is equal to that of their corresponding sides. Then we will find the ratio of the areas, that is, $\dfrac{ar(ABC)}{ar(A'B'C')}$ . Using the previous results we will reach the needed proof.

Complete step by step answer:
We have to prove that the ratio of areas of $ABC$ and \[A'B'C'\] is equal to the square of the ratio of their corresponding sides.
Given that the triangles $ABC$ and \[A'B'C'\] are similar.
Therefore, the ratio of their median is equal to the ratio of the corresponding sides.
That is, $\dfrac{CD}{C'D'}=\dfrac{AB}{A'B'}...(i)$
Now, let us consider the ratios of areas of these triangles. That is,
$\dfrac{ar(ABC)}{ar(A'B'C')}$
We know that area of a triangle $=\dfrac{1}{2}\times base\times height$ .
Therefore, $\dfrac{ar(ABC)}{ar(A'B'C')}=\dfrac{\dfrac{1}{2}\times AB\times CD}{\dfrac{1}{2}\times A'B'\times C'D'}$
Let us cancel the common terms. Thus the above equation becomes
$\dfrac{ar(ABC)}{ar(A'B'C')}=\dfrac{AB\times CD}{A'B'\times C'D'}$
Now let us split the terms as shown below.
$\dfrac{ar(ABC)}{ar(A'B'C')}=\dfrac{AB}{A'B'}\times \dfrac{CD}{C'D'}$
Let us use the equation $(i)$ here. So the above equation becomes
$\dfrac{ar(ABC)}{ar(A'B'C')}=\dfrac{CD}{C'D'}\times \dfrac{CD}{C'D'}$
This can be written as
$\dfrac{ar(ABC)}{ar(A'B'C')}={{\left( \dfrac{CD}{C'D'} \right)}^{2}}$
It is given that the ratio between $CD$ and $C'D'$ is $2:1$ .
Therefore, $\dfrac{ar(ABC)}{ar(A'B'C')}={{\left( \dfrac{2}{1} \right)}^{2}}=\text{square of ratio of the corresponding sides of the two triangles}$
Hence, the ratio of areas of $ABC$ and \[A'B'C'\] is equal to the square of the ratio of their corresponding sides.
Hence proved.

Note: We can also use sides other than $AB$ and \[A'B'\] since all the corresponding sides are equal and are in the ratio of $2:1$. This is done as the question implies that the two triangles are similar. If any such hints are not specified in the question, we will have to prove that the given triangles are similar and then proceed with the above steps.