
The refractive index of the core of an optical fiber is $ {\mu _2} $ and that of the cladding is $ {\mu _1} $ . The angle of incidence on the face of the core so that the light ray just undergoes total internal reflection at the cladding is:
(A) $ {\sin ^{ - 1}}\left( {\dfrac{{{\mu _2}}}{{{\mu _1}}}} \right) $
(B) $ {\sin ^{ - 1}}\sqrt {{\mu _2}^2 - {\mu _1}^2} $
(C) $ {\sin ^{ - 1}}\sqrt {{\mu _2} - {\mu _1}} $
(D) $ {\sin ^{ - 1}}\sqrt {{\mu _1}^2 + {\mu _2}^2} $
Answer
460.8k+ views
Hint To solve this question, we have to apply the phenomenon of total internal reflection on the light rays entering into an optical fiber. We have to obtain the angle of incidence in terms of the refractive indices of the core and the cladding to get the final answer.
Formula used: In this solution we will be using the following formula,
$ {\mu _1}\sin i = {\mu _2}\sin r $
where $ {\mu _1} $ is the refractive index of the medium where the ray is incident with the angle of incidence $ i $ .
$ {\mu _2} $ is the refractive index of the medium where the ray is refracted with the angle of refraction $ r $ .
Complete step by step solution:
Consider the given optical fiber as shown in the figure below. According to the question, the refractive index of the core is $ {\mu _2} $ and that of the cladding is $ {\mu _1} $ .
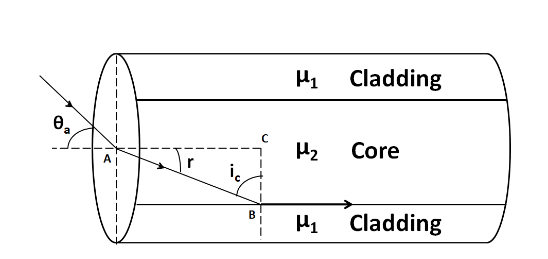
Applying the Snell’s law at the point A, we get
$1 \times \sin {\theta _a} = {\mu _2}\sin r $
$\Rightarrow \sin {\theta _a} = {\mu _2}\sin r $ …………...(1)
Now, for the total internal reflection to take place, the light ray refracted from point A should be incident at an angle equal to the critical angle of incidence at point B.
$\Rightarrow \therefore \angle ABC = {i_C} $
In the triangle ABC, from the angle sum property we have
$\Rightarrow r + {i_c} + {90^ \circ } = {180^ \circ } $
$\Rightarrow r + {i_c} = {90^ \circ } $
So we get the angle of refraction as
$\Rightarrow r = {90^ \circ } - {i_c} $ ……………….(2)
Substituting (2) in (1) we get
$\Rightarrow \sin {\theta _a} = {\mu _2}\sin \left( {{{90}^ \circ } - {i_c}} \right) $
We know that $ \sin \left( {{{90}^ \circ } - \theta } \right) = \cos \theta $ . Therefore
$\Rightarrow \sin {\theta _a} = {\mu _2}\cos {i_c} $
Dividing by $ {\mu _2} $ we get
$\Rightarrow \cos {i_c} = \dfrac{{\sin {\theta _a}}}{{{\mu _2}}} $ ……………..(3)
Now, applying the Snell’s law at the point B, we have
$\Rightarrow {\mu _2} \times \sin {i_c} = {\mu _1}\sin {90^ \circ } $
$\Rightarrow {\mu _2}\sin {i_c} = {\mu _1} $
Dividing by $ {\mu _2} $ we get
$\Rightarrow \sin {i_c} = \dfrac{{{\mu _1}}}{{{\mu _2}}} $ ………………….(4)
On squaring and adding (3) and (4) we have
$\Rightarrow {\cos ^2}{i_c} + {\sin ^2}{i_c} = {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} + {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
We know that $ {\cos ^2}\theta + {\sin ^2}\theta = 1 $ . So we have
$\Rightarrow 1 = {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} + {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
$\Rightarrow {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} = 1 - {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
Multiplying both sides by $ {\mu _2}^2 $ we have
$\Rightarrow {\sin ^2}{\theta _a} = {\mu _2}^2 - {\mu _1}^2 $
Taking square root both the sides
$\Rightarrow \sin {\theta _a} = \sqrt {{\mu _2}^2 - {\mu _1}^2} $
Finally, taking sine inverse both the sides, we get
$\Rightarrow {\theta _a} = {\sin ^{ - 1}}\sqrt {{\mu _2}^2 - {\mu _1}^2} $
Thus, the angle of incidence on the face of the core is equal to $ {\sin ^{ - 1}}\sqrt {{\mu _2}^2 - {\mu _1}^2} $ .
Hence, the correct answer is option B.
Note:
We must note that we have assumed the medium outside the optical fiber to be air, so the refractive index is taken as unity. The reason is that nothing related to the outside medium is mentioned. And in such a situation, the medium has to be taken as air unless stated otherwise.
Formula used: In this solution we will be using the following formula,
$ {\mu _1}\sin i = {\mu _2}\sin r $
where $ {\mu _1} $ is the refractive index of the medium where the ray is incident with the angle of incidence $ i $ .
$ {\mu _2} $ is the refractive index of the medium where the ray is refracted with the angle of refraction $ r $ .
Complete step by step solution:
Consider the given optical fiber as shown in the figure below. According to the question, the refractive index of the core is $ {\mu _2} $ and that of the cladding is $ {\mu _1} $ .

Applying the Snell’s law at the point A, we get
$1 \times \sin {\theta _a} = {\mu _2}\sin r $
$\Rightarrow \sin {\theta _a} = {\mu _2}\sin r $ …………...(1)
Now, for the total internal reflection to take place, the light ray refracted from point A should be incident at an angle equal to the critical angle of incidence at point B.
$\Rightarrow \therefore \angle ABC = {i_C} $
In the triangle ABC, from the angle sum property we have
$\Rightarrow r + {i_c} + {90^ \circ } = {180^ \circ } $
$\Rightarrow r + {i_c} = {90^ \circ } $
So we get the angle of refraction as
$\Rightarrow r = {90^ \circ } - {i_c} $ ……………….(2)
Substituting (2) in (1) we get
$\Rightarrow \sin {\theta _a} = {\mu _2}\sin \left( {{{90}^ \circ } - {i_c}} \right) $
We know that $ \sin \left( {{{90}^ \circ } - \theta } \right) = \cos \theta $ . Therefore
$\Rightarrow \sin {\theta _a} = {\mu _2}\cos {i_c} $
Dividing by $ {\mu _2} $ we get
$\Rightarrow \cos {i_c} = \dfrac{{\sin {\theta _a}}}{{{\mu _2}}} $ ……………..(3)
Now, applying the Snell’s law at the point B, we have
$\Rightarrow {\mu _2} \times \sin {i_c} = {\mu _1}\sin {90^ \circ } $
$\Rightarrow {\mu _2}\sin {i_c} = {\mu _1} $
Dividing by $ {\mu _2} $ we get
$\Rightarrow \sin {i_c} = \dfrac{{{\mu _1}}}{{{\mu _2}}} $ ………………….(4)
On squaring and adding (3) and (4) we have
$\Rightarrow {\cos ^2}{i_c} + {\sin ^2}{i_c} = {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} + {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
We know that $ {\cos ^2}\theta + {\sin ^2}\theta = 1 $ . So we have
$\Rightarrow 1 = {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} + {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
$\Rightarrow {\left( {\dfrac{{\sin {\theta _a}}}{{{\mu _2}}}} \right)^2} = 1 - {\left( {\dfrac{{{\mu _1}}}{{{\mu _2}}}} \right)^2} $
Multiplying both sides by $ {\mu _2}^2 $ we have
$\Rightarrow {\sin ^2}{\theta _a} = {\mu _2}^2 - {\mu _1}^2 $
Taking square root both the sides
$\Rightarrow \sin {\theta _a} = \sqrt {{\mu _2}^2 - {\mu _1}^2} $
Finally, taking sine inverse both the sides, we get
$\Rightarrow {\theta _a} = {\sin ^{ - 1}}\sqrt {{\mu _2}^2 - {\mu _1}^2} $
Thus, the angle of incidence on the face of the core is equal to $ {\sin ^{ - 1}}\sqrt {{\mu _2}^2 - {\mu _1}^2} $ .
Hence, the correct answer is option B.
Note:
We must note that we have assumed the medium outside the optical fiber to be air, so the refractive index is taken as unity. The reason is that nothing related to the outside medium is mentioned. And in such a situation, the medium has to be taken as air unless stated otherwise.
Recently Updated Pages
Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

In case of conflict between fundamental rights of citizens class 7 social science CBSE

Using the following information to help you answer class 12 chemistry CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE

How much time does it take to bleed after eating p class 12 biology CBSE




