Question

The refractive index of water is 4 / 3 and that of glass is 5/3. What will be the critical angle for the ray of light entering water from the glass?
(A). ${{\sin }^{-1}}(\dfrac{4}{5})$
(B). ${{\sin }^{-1}}(\dfrac{5}{4})$
(C). ${{\sin }^{-1}}(\dfrac{1}{2})$
(D). ${{\sin }^{-1}}(\dfrac{2}{1})$

Answer 1

Hint: Refractive index is nothing but disturbance which is caused to wave while it is travelling. Notice that ray is incident on glass and pass through water. Direction of the ray is important. The term critical angle is in Snell’s law. Use Snell’s law formula.

Complete step by step answer:

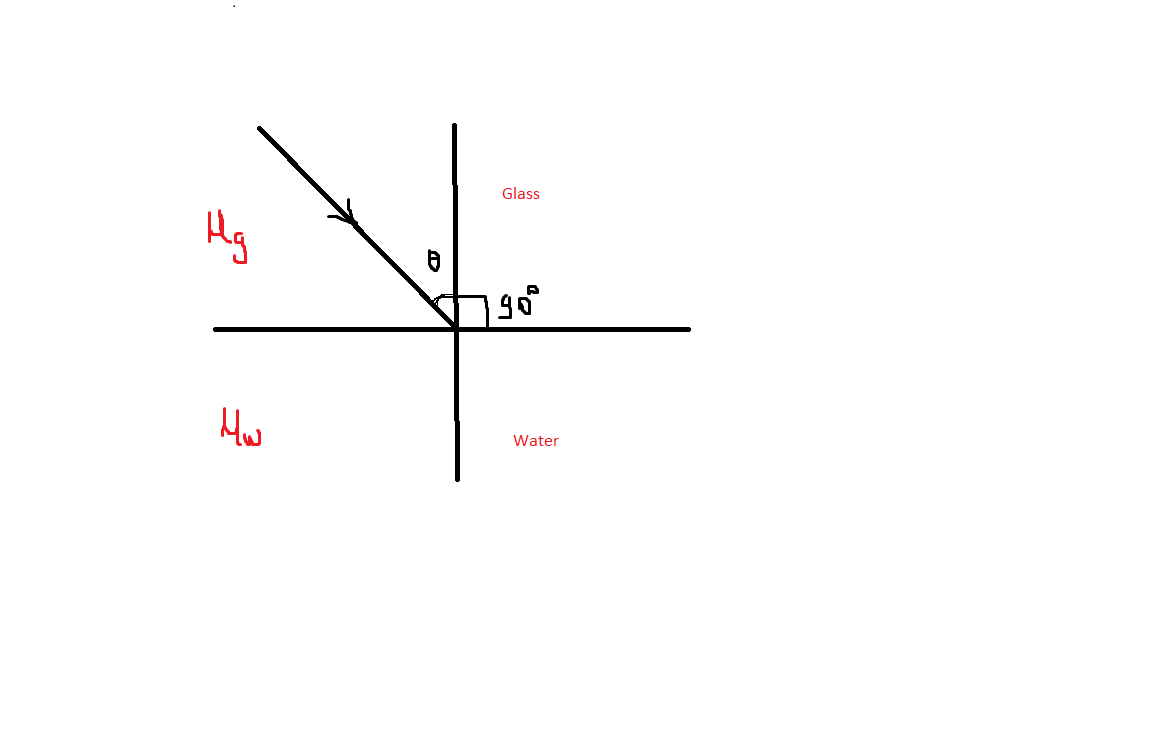
According to Snell’s law,
${{\mu }_{g}}\sin {{\theta }_{1}}={{\mu }_{w}}\sin {{\theta }_{2}}$
Where,
${{\mu }_{g}}$= refractive index of glass
${{\mu }_{w}}$= refractive index of water
\[{{\theta }_{1}}\]= incident angle or critical angle
\[{{\theta }_{2}}\]= refracted angle
Put the value of the refractive index of water and glass. Angle of refraction in water must be the right angle as you can see in the picture.
We get,
$\begin{align}
  & \dfrac{5}{3}\sin \theta =\dfrac{4}{3}\sin 90 \\
 & \sin \theta =\dfrac{\dfrac{4}{3}}{\dfrac{5}{3}} \\
 & \theta ={{\sin }^{-1}}\dfrac{4}{5} \\
\end{align}$
Value of sin of 90 degrees is one.

Hence, the correct option is (A).

Note: Snell’s law tells the relationship between incident angle and refracted angle along with refractive index of both the medium. Angle between normal and ground will always be the right angle. Here is the tip that whenever you hear respectively then consider that each one value is assigned to different-different quantities but in a sequential manner. You can see this in the question explanation line. From the question you can see that the refractive index of glass is more than water. Hence we can say that it has high density and therefore it will cause more disturbance to wave.