Question

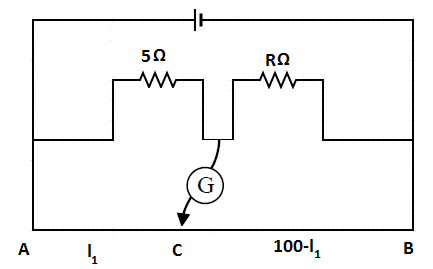
The resistance in the two arms of the meter bridge are \[\text{5 }\!\!\Omega\!\!\text{ }\] and \[\text{R }\!\!\Omega\!\!\text{ }\], respectively. When the resistance \[\text{R}\] is shunted with an equal resistance, the new balance point is at\[1.6{{l}_{1}}\]. The resistance \[\text{R}\] is

A\[\text{10 }\!\!\Omega\!\!\text{ }\]
B\[\text{15 }\!\!\Omega\!\!\text{ }\]
C\[\text{20 }\!\!\Omega\!\!\text{ }\]
D\[\text{25 }\!\!\Omega\!\!\text{ }\]

Answer 1

Hint: We know that a meter bridge is used to determine the unknown resistance. The unknown resistance can be calculated from the equation which relates the unknown and known resistances and the length of wire. Here, a resistor is shunted with another resistor of equal resistance. Hence, the total resistance across the terminals is changed, so is the balancing point. First, calculate the new balancing point, and then using the obtained value we can find out the unknown resistance.
Formula used:
\[\dfrac{R}{L}=\dfrac{S}{100-L}\]

Complete step-by-step solution:

Given,
Known resistance, \[R=5\Omega \]
Initial unknown resistance \[=R\Omega \]
New balancing point \[L=1.6{{l}_{1}}\]
We have,
\[\dfrac{R}{L}=\dfrac{S}{100-L}\] --------- 1
Where,
\[R\] is the known resistance
\[S\] is the unknown resistance
Initially, the balancing point is at \[{{l}_{1}}\].
Substitute the \[R=5\Omega \] and \[L={{l}_{1}}\] in equation 1, we get,
\[\dfrac{5}{{{l}_{1}}}=\dfrac{S}{100-{{l}_{1}}}\] ----------- 2
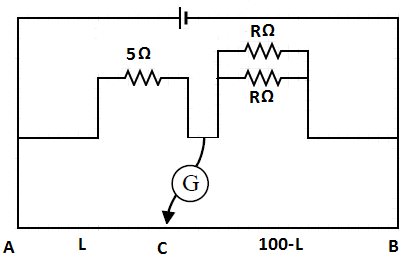
When the resistance \[R\] is shunted with an equal resistance \[R\], the resistance in
that arm becomes \[\dfrac{R}{2}\]
Then,
\[\dfrac{5}{L}=\dfrac{\dfrac{R}{2}}{100-L}\]----------- 3
Substitute the value of \[{{L}_{1}}\] in the equation 3. We get,
\[\dfrac{5}{1.6{{l}_{1}}}=\dfrac{\dfrac{R}{2}}{100-1.6{{l}_{1}}}\]------- 4
Divide equation 2 by 4, then,
\[\dfrac{1.6}{2}=\dfrac{\left( 100-1.6{{l}_{1}} \right)}{100-{{l}_{1}}}\]
\[\Rightarrow 160-1.6{{l}_{1}}=200-3.2{{l}_{1}}\]
\[\Rightarrow 1.6{{l}_{1}}=40\]
\[\Rightarrow {{l}_{1}}=\dfrac{40}{1.6}=25cm\]
Substitute \[{{l}_{1}}=25cm\] in equation 1, we get,
\[\dfrac{5}{25}=\dfrac{R}{100-25}\]
\[\Rightarrow R=15\Omega \]
Hence, the answer is option B.

Note: The meter bridge works based on the same principle as the Wheatstone bridge. It is used to find the unknown resistance. Readings are obtained by moving the jockey on the wire. Mostly the balancing points are obtained around the middle of a meter bridge so that the sensitivity of the meter bridge is increased and thereby no deflection in the galvanometer is obtained.