Question

The rms value of current in an ac circuit is 25A, then peak current is-
A. 35.36 mA
B. 35.36 A
C. 3.536 A
D. 49.38 A

Answer 1

Hint: The peak value is the highest value that waveform reaches and Root mean square value (rms) is the effective value of total waveform. The peak current value is always greater than rms value.

Complete step-by-step answer:
The relation between peak value and rms value of current is given by,
\[{I_0} = \sqrt 2 \times {I_{rms}}\] …..(1)
where, \[{I_0}\] is peak value of current and \[{I_{rms}}\] is root mean square value of current.
Following graph shows the graphical representation of \[{I_0}\] and \[{I_{rms}}\].

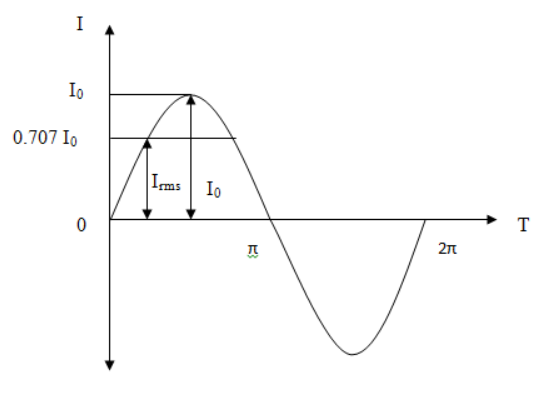
Here, it is given that-
\[{I_{rms}} = 25A\]
and we have to find peak value current, using equation (1) we get,
\[{I_0} = \sqrt 2 \times 25\]
\[{I_0} = 35.3553\]
So, the peak value of current is 35.3553 A i.e. \[{I_0} = 35.3553\]
The correct answer is option B.
Additional information:
This relation of rms and peak value is also used in case of voltage.
\[{V_{rms}} = 0.707 \times {V_0}\]
Here, we can show the graphical representation of peak value and root mean square value of voltage with the time period as it is shown in solution for current.

Note: There are two standard forms of the relation between peak value and rms value of current but having same meaning,
\[{I_0} = \sqrt 2 \times {I_{rms}}\] and \[{I_{rms}} = 0.707 \times {I_0}\]