Question

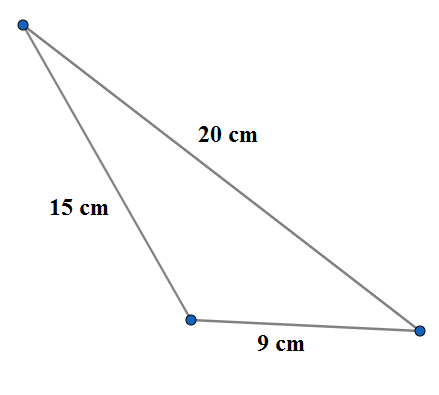
The semi perimeter of a triangle having the length of its sides as 20 cm, 15 cm and 9 cm is : \[\]
A.44 cm\[\]
B.21 cm\[\]
C.22 cm\[\]
D.24 cm\[\]

Answer 1

Hint: We recall the dentition of length of sides of a triangle, the perimeter of the triangle and then semi-perimeter. We add the given lengths of triangles to get the perimeter of the triangle and divide the perimeter by 2 to get the semi-perimeter. \[\]

Complete step by step answer:
We know that the perimeter of any geometrical shape in a plane is the length of outline of the shape. We know that the triangle is a polygon with three vertices and the lien segment which joins those vertices are called sides. The distance between two vertices is called the length of the side. \[\]
The outline of the triangle is the three sides of the triangle. The perimeter of the triangle is the length of the whole outline that is the sum of the lengths of the sides of a triangle. If $a,b,c$are the lengths of triangle ABC is drawn below, then the perimeter of the triangles is denoted as P and is given by the formula
\[P=a+b+c\]

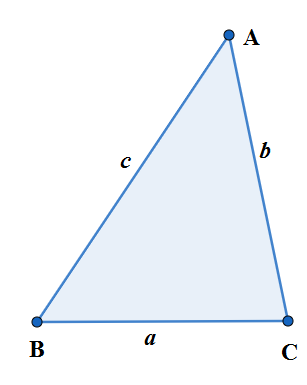
We know that the word ‘semi’ means half. That is why the word semi-perimeter means half of the perimeter. The semi-perimeter of triangle is generally denoted as $s$ and is given by
\[s=\dfrac{P}{2}=\dfrac{a+b+c}{2}\]
We are given in the question the length of three sides of the triangle sides as 20 cm, 15 cm and 9 cm. We can assign in our choice $a=20$ cm, $b=15$cm and $c=9$cm. So the semi-perimeter of the triangle is
\[s=\dfrac{a+b+c}{2}=\dfrac{20+15+9}{2}=\dfrac{44}{2}=22\text{ cm}\]

So, the correct answer is “Option C”.

Note: We can use the semi-perimeter of the triangle to find the area of the triangle using the formula $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$. We must remember that the semi-perimeter is in the same unit as length but the area is in the square unit of the length. We can find the semi-perimeter of an equilateral triangle as $\dfrac{3a}{2}$ where $a$ is the length of the side.