Question

The terminal arm is in II (second) quadrant, what is the possible measure of an angle?

Answer 1

Hint: We solve this problem by considering the quadrants of the plane. The quadrants of the plane are divided into four quadrants namely I (first), II (second), III (third), IV (fourth) quadrants. These quadrants are formed by dividing the total angle \[{{360}^{0}}\]into four regions of \[{{90}^{0}}\]each as shown below. By using this we can calculate the required result.

Complete step-by-step answer:

We are given that the terminal arm is in II (second) quadrant.
Let us assume that the initial arm lies on the horizontal axis.
We know that the quadrants are divided into four types by dividing the total angle \[{{360}^{0}}\]into four regions of \[{{90}^{0}}\]each.
Let us assume that the initial arm is positioned as follows

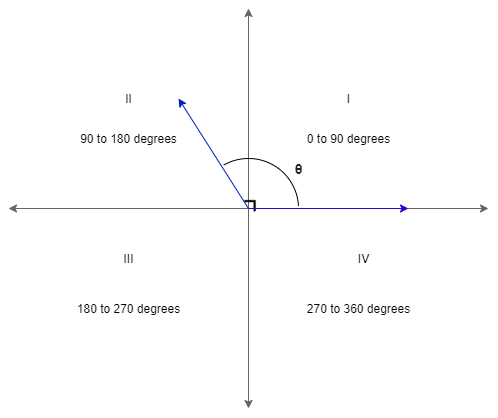
Here, let us assume that the blue coloured line is the initial arm.
We are given that the terminal arm is in II (second) quadrant.
We know that the second quadrant has angles from \[{{90}^{0}}\]to \[{{180}^{0}}\].
So, we can say that is the terminal arm is in II (second) quadrant the possible measure of an angle is from \[{{90}^{0}}\]to \[{{180}^{0}}\].
Therefore, the answer can be written as
 \[\Rightarrow \theta \in \left( {{90}^{0}},{{180}^{0}} \right)\]

Note: Students may get confused in the initial arm position. We are given that the terminal arm is in II (second) quadrant but we are not given anything about the initial arm. In that case we take the general type that is considering that the initial arm is in the horizontal axis as mentioned above. So, students may consider their own cases but in general we take standard type when there is no information mentioned about the initial arm.