
The two legs of a right triangle are equal and the square of its hypotenuse is 50. Find the length of each leg.
Answer
492.6k+ views
1 likes
Hint: Let x be the length of two legs which are equal in length.
It is given that the square of the hypotenuse is 50.
Thus, find the length of two legs using Pythagoras’ theorem.
Complete step-by-step answer:
It is given that the legs of a right triangle are equal and the square of its hypotenuse is 50.
Let the length of the same legs of the right triangle be x.
So, by using the Pythagoras’ theorem, we can find the length of the same two legs.
The Pythagoras’ theorem is stated as, the square of hypotenuse is the sum of squares of the remaining two sides of the triangle.
It is given that the square of the hypotenuse is 50.
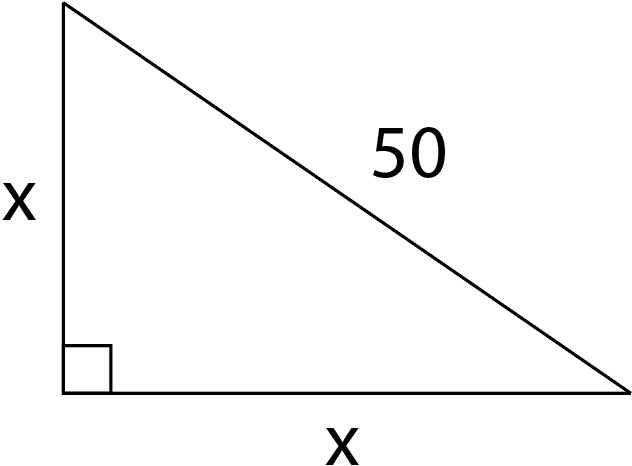
Here, x = -5 is not possible because x is the length of a side and length of a side cannot be negative.
Thus,
Therefore, the length of each leg is 5 units.
Note: Pythagoras’ Theorem:
In a right angle triangle, the square of the hypotenuse is the sum of the squares of the remaining two sides.
Here, hypotenuse is the longest side of the triangle.
For example,
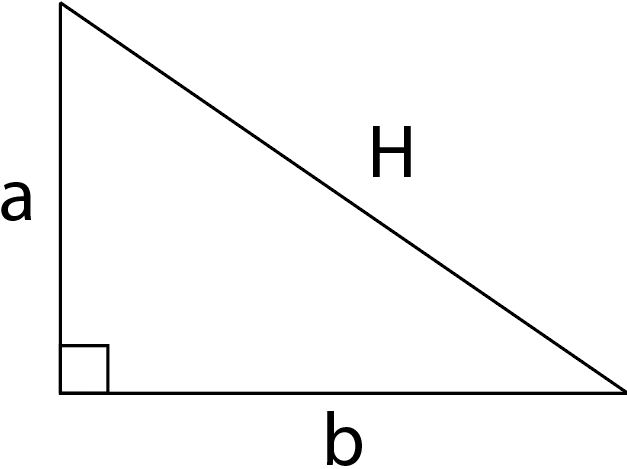
The Pythagoras’ theorem for the above diagram will be
It is given that the square of the hypotenuse is 50.
Thus, find the length of two legs using Pythagoras’ theorem.
Complete step-by-step answer:
It is given that the legs of a right triangle are equal and the square of its hypotenuse is 50.
Let the length of the same legs of the right triangle be x.
So, by using the Pythagoras’ theorem, we can find the length of the same two legs.
The Pythagoras’ theorem is stated as, the square of hypotenuse is the sum of squares of the remaining two sides of the triangle.
It is given that the square of the hypotenuse is 50.

Here, x = -5 is not possible because x is the length of a side and length of a side cannot be negative.
Thus,
Therefore, the length of each leg is 5 units.
Note: Pythagoras’ Theorem:
In a right angle triangle, the square of the hypotenuse is the sum of the squares of the remaining two sides.
Here, hypotenuse is the longest side of the triangle.
For example,

The Pythagoras’ theorem for the above diagram will be
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

What does R mean in math class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE





