Question

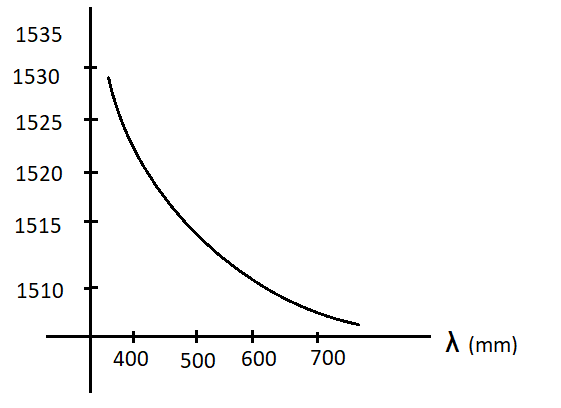
The variation of the refractive index of a crown glass thin prism with the wavelength of the light is shown. Which of the following graphs is the correct one, if the ${D_m}$ is the angle of minimum deviation?

A)
 

B)

C)

D)

Answer 1

Hint: The above problem is based on the concept of the angle of deviation. The angle of deviation varies with the variation in the refractive index. If the incidence angle and refraction angle are the same then the light bends minimum and angle is called angle of minimum deviation.

Complete step by step answer:
The expression of angle of minimum deviation is given as,
${D_m} = 2{\sin ^{ - 1}}\left( {n\sin \left( {\dfrac{A}{2}} \right)} \right) - A$
Here, n is the refractive index, A is the angle of the prism.
As we can observe from the above expression that the angle of minimum deviation varies with the refractive index. If the value of the refractive index increases then the angle of minimum deviation also increases.
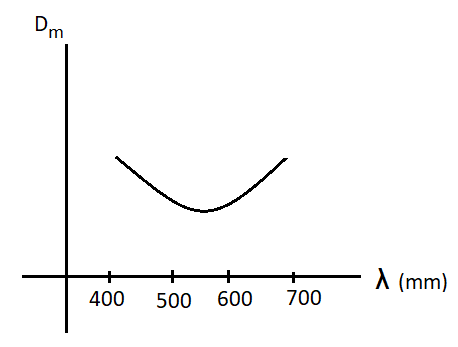
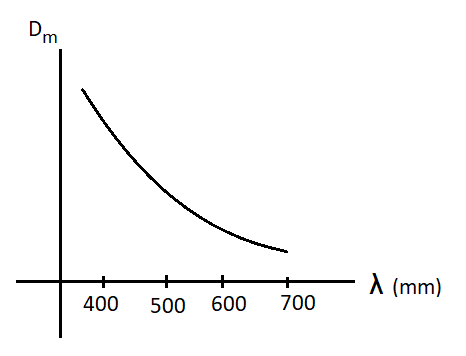
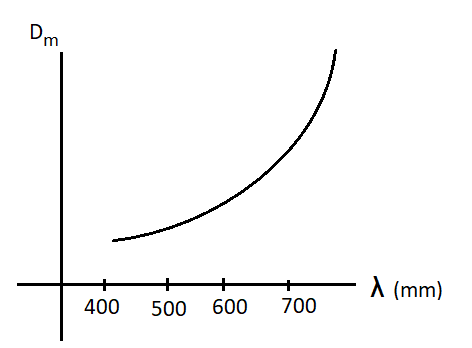
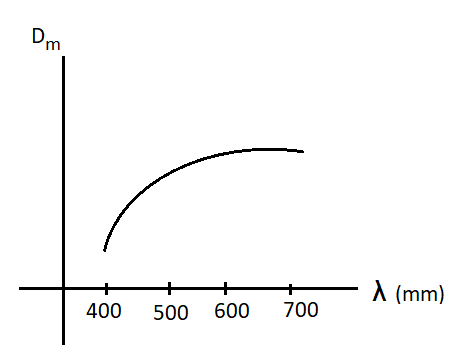
The angle of minimum deviation in the graph of option (B) varies according to the refractive index of crown thin glass, so the option (B) is correct and other options are incorrect.

Therefore, the option (B) is correct.

Additional Information:
If the refractive index of the medium is more than the medium of incident ray then the angle of minimum deviation increases and decreases if the refractive index is lower than the refractive index of the incident medium.

Note: The refractive index of the incident medium may change due to variation in outside condition, so angle of minimum deviation should be calculated in stable conditions. The speed, wavelength and frequency of the light also vary with the variation in the refractive index. The speed of the light remains more in the rare medium than the speed of light in a dense medium.