Question

The volume of the tetrahedron formed by the points \[\left( {{\rm{1}},{\rm{1}},{\rm{1}}} \right),\left( {{\rm{2}},{\rm{1,3}}} \right),\left( {{\rm{3}},{\rm{2}},{\rm{2}}} \right)\] and \[\left( {{\rm{3}},{\rm{3}},{\rm{4}}} \right)\] in cubic units is
\[\begin{array}{l}A.\,\,\dfrac{5}{6}\\B.\,\,\dfrac{6}{5}\\C.\,\,5\\D.\,\,\dfrac{2}{3}\end{array}\]

Answer 1

Hint: First assume 4 variables to give 4 points in the question. Now by difference between pairs of points, repeat it with keeping the first point in common. Find the 3 possible sides. Now you have 3 vectors from one point which form a tetrahedron. Now find the base area and height of this tetrahedron. Then substitute them into the formula of volume of tetrahedron in terms of base area B, height h, given by V: \[V{\rm{ = }}\dfrac{1}{3} \times B \times h\]

Complete step by step solution:
The 4 points given in the question, can be written in the form:
(1,1,1), (2,1,3), (3,2,2) and (3,3,4)
Let us assume first point to be denoted by A, we get it as \[{\rm{A}} = \left( {{\rm{1}},{\rm{1}},{\rm{1}}} \right)\]
Let us assume first point to be denoted by B, we get it as \[{\rm{B}} = \left( {{\rm{2}},{\rm{1}},{\rm{3}}} \right)\]
Let us assume first point to be denoted by C, we get it as \[{\rm{C}} = \left( {{\rm{3}},{\rm{2}},{\rm{2}}} \right)\]
Let us assume first point to be denoted by D, we get it as \[{\rm{D}} = \left( {{\rm{3}},{\rm{3}},{\rm{4}}} \right)\]
Now drawing tetrahedron with ABCD vertices we get it as

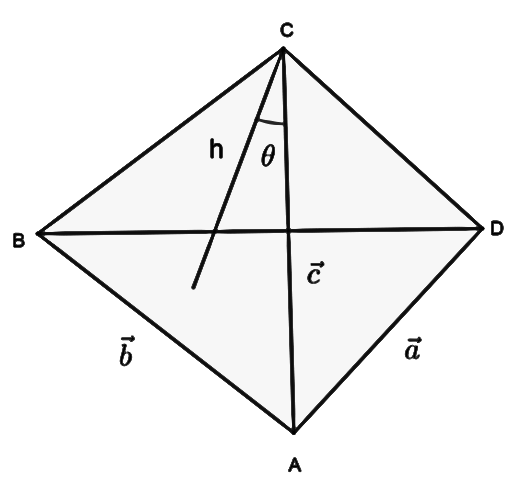
Let us assume vector \[\vec b\] is the side AB.
Let us assume vector \[\vec a\] is the side AD.
Let us assume the vector \[\vec c\] is the side AC.
Let us assume h is the height of the tetrahedron and also assume that height makes angle \[\theta \] with \[\vec c\].
By the above assumption, we can say height is written as:
\[\vec h{\rm{ = \vec c cos}}\theta \]
As the base is triangle ABD, we can write base area as:
\[Base{\rm{ area = }}\dfrac{1}{2}\left| {\vec a \times \vec b} \right|\]
By basic geometry knowledge, we know that the volume (V) is:
\[V{\rm{ = }}\dfrac{1}{3}\left( {base{\rm{ area}}} \right) \times \left( {height} \right)\]
By substituting values of base area and height, we get
\[Volume{\rm{ = }}\dfrac{1}{6}{\rm{ }}\left| {\vec a \times \vec b} \right|{\rm{ }}{\rm{. }}\left| {\vec c} \right|{\rm{ }}Cos\theta \]
The form of \[\left| a \right|{\rm{ }}\left| b \right|{\rm{ Cos}}\theta {\rm{ }}\]is written as \[\vec a{\rm{ }}{\rm{. }}\vec b\]. So, we get
\[Volume{\rm{ = }}\dfrac{1}{6}\left[ {\left( {\vec a \times \vec b} \right){\rm{ }}{\rm{. }}\vec c} \right]\]
In our question we can find sides AB, AC, AD as follows:
Side AB is found by (denote it as \[\vec b\]), we get it as:
AB = B-A
By substituting points, we get the equation as follows:
\[\vec b{\rm{ = }}\left( {2,1,3} \right) - \left( {1,1,1} \right){\rm{ = }}\left( {1,0,2} \right)\]
Similarly we know the side AC as C-A, by substituting
\[\vec c{\rm{ = }}\left( {3,2,2} \right) - \left( {1,1,1} \right){\rm{ = }}\left( {2,1,1} \right)\]
Similarly we know the side AD as D-A, by substituting
\[\vec a{\rm{ = }}\left( {3,3,4} \right) - \left( {1,1,1} \right){\rm{ = }}\left( {2,2,3} \right)\]
By substituting this into volume formula, we get it as:
\[V{\rm{ = }}\dfrac{1}{6}\left( {\left( {\bar a \times \bar b} \right){\rm{ }}{\rm{. \bar c}}} \right)\]
The above can be written as scalar triple product, we get:
\[V{\rm{ = }}\dfrac{1}{6}\left( {\begin{array}{*{20}{c}}1&0&2\\2&1&1\\2&2&3\end{array}} \right)\]
\[V = {\rm{ }}\dfrac{1}{6}\left( {1\left( {3 - 2} \right) + 0 + 2\left( {4 - 2} \right)} \right)\]
By simplifying the above, we get: \[V{\rm{ = }}\dfrac{1}{6}\left( {1 + 4} \right){\rm{ = }}\dfrac{5}{6}\]
Volume is \[\dfrac{5}{6}\] cubic units.
Therefore, option (a) is correct.

Note: Be careful while substituting the points, as that is the only main step to reach to answer. The idea of converting the given into a scalar triple product makes it a single step or else you should do a cross product and then again a dot product which is a long method. Anyways you get the same result.