Question

There is a point inside a circle, what is the probability that this point is closer to the circumference than to the centre?
A. \[\dfrac{3}{4}\]
B. \[\dfrac{1}{2}\]
C. \[\dfrac{1}{4}\]
D. \[\dfrac{1}{3}\]

Answer 1

Hint: Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of the circle defines the region occupied by it. Area of any circle is the region enclosed by the circle itself or the space covered by the circle. The formula to find the area of the circle is = \[\pi {r^2}\] and for point to be close to the circumference than to the centre the point must be at a distance greater than \[\dfrac{r}{2}\] from the centre of circle.

Complete step by step solution:
Total possible outcomes = Area of circle = \[\pi {r^2}\]
And let the radius of the circle be 'r'. Observe the figure, we have to find the probability of point, P in the ring which will be closer to circumference. For point to be close to the circumference than to the centre the point must be at a distance greater than \[\dfrac{r}{2}\] from the centre of circle where r is the radius, in which in the figure \[r = \dfrac{r}{2}\].

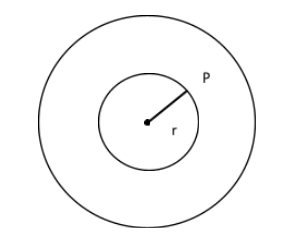
Area of ring = Area of outer circle - Area of inner circle
Area of ring = \[\pi {r^2} - \pi {\left( {\dfrac{r}{2}} \right)^2}\]
Area of ring= \[\pi {r^2} - \dfrac{{\pi {r^2}}}{4}\]
Therefore, the outcome is \[\dfrac{{3\pi {r^2}}}{4}\].
Area of region of a point such that distance is greater than \[\dfrac{r}{2}\] from the centre of circle = \[\dfrac{{3\pi {r^2}}}{4}\]
Hence, the Probability that this point is close to the circumference than to the centre is
\[\dfrac{{\dfrac{{3\pi {r^2}}}{4}}}{{\pi {r^2}}}\] = \[\dfrac{3}{4}\]

Therefore, option A is the right answer.

Note: The key point to find the probability in which the point is close to the circumference than to the centre, we can consider the area of the region of the point with respect to area of circle and the distance surrounding a circle is known as the circumference of the circle. The diameter is the distance across a circle through the centre, and it touches the two points of the circle perimeter.