Question

Three 60W (120V) light bulbs are connected across a 120V power line shown in figure

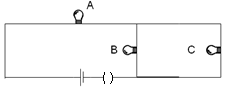
Find
(a) the voltage across each bulb and
(b) the total power dissipated in the three bulbs
A) a) 90 V,40 V, 40 V; (b)40 W
B) a) 80 V,40 V, 40 V; (b)40 W
C) a) 80 V,50 V, 40 V; (b)40 W
D) a) 80 V,40 V, 40 V; (b)50 W

Answer 1

Hint We need to find the resistance of the bulbs using the ratings of power and voltage provided for the bulbs. Then we have to calculate the net current in the circuit using ohm’s law and then the distribution of voltages across the bulbs.

Formula used: In this solution we will be using the following formula,
 $\Rightarrow P = \dfrac{{{V^2}}}{R} $ where $ P $ is the power rating of the bulb, $ V $ is the voltage rating, and $ R $ is its resistance.
Ohm’s law: $ V = IR $ where $ I $ is the current flowing through the bulb.

Complete step by step answer
To find the voltage drops across the bulbs, we must first find the current flowing in the circuit for which we need to find the resistance of the bulbs. The resistance of the bulbs can be calculated using the rating of the bulbs which are provided as 60W (120V). Using the relation
 $\Rightarrow P = \dfrac{{{V^2}}}{R} $
We can write
 $\Rightarrow 60 = \dfrac{{{{120}^2}}}{R} $
 $\Rightarrow R = 240\,\Omega $ which is the resistance of all the three identical bulbs.
Now B and C bulbs are in parallel and their combination is in series with A. So, the net resistance of B and C is
 $\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{{R_B}}} + \dfrac{1}{{{R_C}}} $
 $\Rightarrow \dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{240}} + \dfrac{1}{{240}} $
Which gives us,
 $\Rightarrow {R_{BC}} = 120\,\Omega $
The net combination of BC will be in series with A so we have the net resistance as
 $\Rightarrow {R_{net}} = 120 + 240 $
 $\Rightarrow {R_{net}} = 360\,\Omega $
The current in the circuit can then be determined using ohm’s law as
 $\Rightarrow I = \dfrac{V}{R} $
On substituting the values,
 $\Rightarrow I = \dfrac{{120}}{{360}} = \dfrac{1}{3}A $
Now, when the current flows in the circuit, the current through bulb A will be $ {I_A} = 1/3A $ but the current will split into two equal parts as their resistance is equal. So $ {I_B} = 1/6\,A $ and $ {I_C} = 1/6A $ .
a) We can now calculate the voltage drop across all the 3 bulbs.
For bulb A, using ohm’s law, $ {V_A} = {I_A}R $
  $\Rightarrow {V_A} = \dfrac{1}{3} \times 240 = 80\,V $
For bulb B, $ {V_B} = {I_B}R $
  $\Rightarrow {V_B} = \dfrac{1}{6} \times 240 = 40\,V $
Similarly, for bulb C, $ {V_C} = {I_C}R $
 $\Rightarrow {V_C} = \dfrac{1}{6} \times 240 = 40V $
b) The power dissipated across the bulbs can be calculated using the relation $ P = {I^2}R $
For bulb A: $ {P_A} = {I_A}^2R $
 $\Rightarrow {P_A} = \dfrac{1}{9} \times 240 = \dfrac{{80}}{3}\,W $
Similarly, for bulb B: $ {P_B} = \dfrac{1}{{36}} \times 240 $
  $\Rightarrow {P_B} = \dfrac{{20}}{3}W $
And for bulb C: $ {P_C} = \dfrac{1}{{36}} \times 240 $
 $\Rightarrow {P_C} = \dfrac{{20}}{3}W $
Hence the total power dissipated across all the bulbs will be
 $\Rightarrow {P_{total}} = \dfrac{{80}}{3} + \dfrac{{20}}{3} + \dfrac{{20}}{3} $
 $\Rightarrow 40\,W $
Hence the correct choice is option (B).

Note
Since bulbs B and C are in parallel, they will have the same voltage drop across them which can help us in eliminating option (C) as the possible answer. While the total current in the circuit will flow across in bulb A since it is connected directly with the battery however for bulbs B and C, the total current will split in half when flowing through those two bulbs.