Question

Three charges (each Q) are placed at the three corners of an equilateral triangle. The fourth charge q is placed at the centre of the triangle. The ratio |q/Q| so as to make the system in equilibrium is:
A.$1:3$
B.$1:\sqrt{3}$
C.$\sqrt{3}:1$
D.$2:\sqrt{3}$

Answer 1

Hint: To solve this question we need to consider both the charges which are present in the question that is q and Q. Then we have to find the total force at any of the three vertices of the triangle. And after equating them, we will get the required result.

Complete answer:

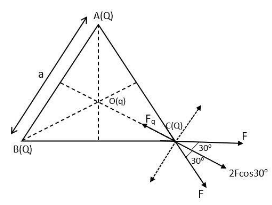
Let us assume an equilateral triangle ABC having AB=BC=CA=a units. Charge Q is placed at three of its vertices and another charge q has been placed at the centre.
We have been given that the system of charges is in equilibrium. So, at any position where the charges have been placed should be balanced.
Let us find out the net force acting on the charge Q positioned at the point C. Since the charges placed at the vertices are of same sign and magnitude, so, the forces exerted by them will be equal in magnitude.
Now, the forces exerted by the two charges placed at vertices A and B will exert equal forces at the charge placed at C, suppose it as F.

We know that the force exerted by a charge particle $q_1$ on another charge particle $q_2$ placed at a distance r is given by $F=\dfrac{kq_1 q_2}{r^2}$
So, the force exerted by the charges Q at vertices A and B, $F=\dfrac{kQ^2}{a^2}$ ………. (i)
And the force exerted by the charge q will be, $F_q =\dfrac{kqQ}{ \left(\dfrac{a}{\sqrt{3}}\right)^2}$.......... (ii) (since $OC=\dfrac{a}{\sqrt{3}}$)

Now, we can see that the vertical component of the forces exerted by charges Q at point C are equal and opposite in nature and for balancing their horizontal component the charge q should be negative in nature.
Thus, we can write that $F_q = 2Fcos30^o$
Substituting the values from equation (i) and (ii), we get

$\dfrac{kqQ}{ \left(\dfrac{a}{\sqrt{3}}\right)^2}=2\times\dfrac{kq_1 q_2}{r^2}cos30^o$
$\dfrac{3kqQ}{ a^2}=2\times\dfrac{kq_1 q_2}{r^2}\times \dfrac{\sqrt{3}}{2}$
$\implies \dfrac{q}{Q}=\dfrac{1}{\sqrt{3}}$

So, the correct answer is “Option B”.

Note:
If we will consider the fourth charge as positive, then the net force at any of the three vertices will not be zero and hence the system will not be in equilibrium. The net force at the centre will be zero as because of the symmetry, since the triangle is an equilateral triangle.