Question

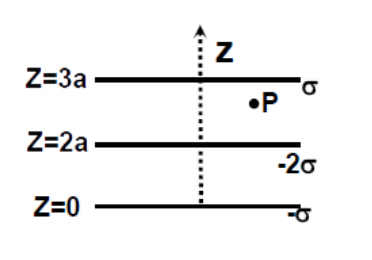
Three infinitely charged sheets are kept parallel to x-plane having charge densities as shown. Then, the value of the electric field at 'P' is

A. $\dfrac{{ - 4\sigma }}{{{\varepsilon _0}}}\hat k$
B. $\dfrac{{4\sigma }}{{{\varepsilon _0}}}\hat k$
C. $\dfrac{{ - 2\sigma }}{{{\varepsilon _0}}}\hat k$
D. $\dfrac{{2\sigma }}{{{\varepsilon _0}}}\hat k$

Answer 1

Hint: For an infinitely charged plane sheet, electric field is given by $E = \dfrac{\sigma }{{2{\varepsilon _0}}}$ .
The total electric field at point ‘$P$’ will be the vector sum of the electric field due to all the three infinitely charged sheets.

Complete answer:
As given in the question, three infinitely charged sheets are kept parallel to x-plane or are kept at $z=0, z=2a$, and $z=3a.$
For an infinite sheet of charge, the electric field will be perpendicular to the surface and given by $E = \dfrac{\sigma }{{2{\varepsilon _0}}}$. This formula is derived by the Gauss Law which states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
Now, the direction of the electric field depends on the sign of surface charged density $\sigma $ and the location of the point $P$. If $\sigma $ is positive then the direction will be towards point $P$.
Let us suppose an upward direction to be positive.
So, the electric field due to the sheet at $z=0$, ${E_{ - \sigma }} = - \dfrac{\sigma }{{2{\varepsilon _0}}}$
Similarly, the electric field due to the sheet at $z=2a$, ${E_{ - 2\sigma }} = - \dfrac{{2\sigma }}{{2{\varepsilon _0}}}$.
And, the electric field due to the sheet at $z=3a$, ${E_\sigma } = - \dfrac{\sigma }{{2{\varepsilon _0}}}$
Now, the total electric field due to the sheets at point P is given by, ${E_P} = {E_{ - \sigma }} + {E_{ - 2\sigma }} + {E_\sigma }$ as a vector sum.
So, ${E_P} = - \dfrac{\sigma }{{2{\varepsilon _0}}} - \dfrac{{2\sigma }}{{2{\varepsilon _0}}} - \dfrac{\sigma }{{2{\varepsilon _0}}}$
On simplification we have, ${E_P} = - \dfrac{{2\sigma }}{{{\varepsilon _0}}}$
Here (–) sign represents the downward or opposite of $\hat k$.

$\therefore$ The the value of electric field at 'P' is ${E_P} = - \dfrac{{2\sigma }}{{{\varepsilon _0}}}$. Hence, the correct option is (C).

Note:
The electric field is a vector quantity. So, carefully determine the direction of the field. Remember that the direction of the electric field depends on the sign of surface charge density $\sigma $ and the location of the point P. If $\sigma $ is positive then the direction will be towards point $P$ and if it is negative then the direction will be away from point $P$.