Question

Three large parallel plates have uniform surface charge densities as shown in the figure. What is the electric field at point $P$ ?

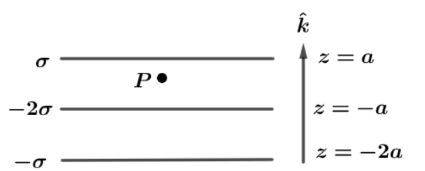
A. $ - \dfrac{{4\sigma }}{{{ \in _0}}}\hat k$
B. $\dfrac{{4\sigma }}{{{ \in _0}}}\hat k$
C. $ - \dfrac{{2\sigma }}{{{ \in _0}}}\hat k$
D. $\dfrac{{2\sigma }}{{{ \in _0}}}\hat k$

Answer 1

Hint: In electrostatics, Electric field due to any point charge at a distant point is defined as the force acting on that point per unit test positive charge and Electric field is a vector quantity. In order to find the net electric field at point $P$ we will calculate the electric field due to individual plates and then add them using the addition rule of vector algebra.

Formula used:
Electric field due to a large sheet having a uniform charge density of $\sigma $ is independent of the point where it’s to be measured and it’s given by
$\vec E = \dfrac{\sigma }{{2{ \in _0}}}\hat n$
where $\hat n$ is the perpendicular direction to the plane of sheet and this direction of electric field is away from the sheet for a positive surface charge density sheet and in the direction towards the sheet if sheet having a negative surface charge density.

Complete step by step answer:
The direction of the electric field at point P due to each plate is shown in the diagram.

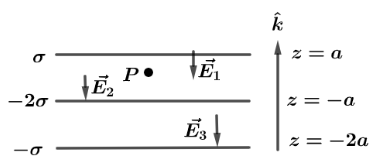
Since point $P$ lies below the plate of surface charge density $ + \sigma $ the, its direction is away from the sheet which is $ - \hat k$. Hence, Electric field due to the first plate is given by ${\vec E_1} = \dfrac{\sigma }{{2{ \in _0}}}( - \hat k)$. For plate second, which have a surface charge density of $ - 2\sigma $ , Point P lies above it and direction of electric field will towards the plate which is $ - \hat k$ hence, electric field due to second plate is given by
${\vec E_2} = \dfrac{{2\sigma }}{{2{ \in _0}}}( - \hat k)$

Now, for third plate Point P lies above the plate and it have a negative surface charge density of $ - \sigma $ Hence, electric field will be in direction towards the plate which is $ - \hat k$ , hence electric field for third plate is given by
${\vec E_3} = \dfrac{\sigma }{{2{ \in _0}}}( - \hat k)$

Now, Net electric field at point P can be calculated by adding the individual electric fields, since all three electric fields are in same direction of $ - \hat k$ so,
${\vec E_{net}} = {\vec E_1} + {\vec E_2} + {\vec E_3}$
On putting the values of ${\vec E_1} = \dfrac{\sigma }{{2{ \in _0}}}( - \hat k)$
${\vec E_2} = \dfrac{{2\sigma }}{{2{ \in _0}}}( - \hat k)$
$\Rightarrow {\vec E_3} = \dfrac{\sigma }{{2{ \in _0}}}( - \hat k)$ We get,
$\Rightarrow {\vec E_{net}} = \dfrac{\sigma }{{2{ \in _0}}}( - \hat k) + \dfrac{{2\sigma }}{{2{ \in _0}}}( - \hat k) + \dfrac{\sigma }{{2{ \in _0}}}( - \hat k)$
$\therefore {\vec E_{net}} = \dfrac{{ - 2\sigma }}{{{ \in _0}}}(\hat k)$
So, net electric field at point P is ${\vec E_{net}} = \dfrac{{ - 2\sigma }}{{{ \in _0}}}(\hat k)$.

Hence, the correct option is C.

Note: It should be remembered that, for large plane sheets having a surface charge density of $\sigma $ , the magnitude of electric field is independent of the distance of the point where it’s measured unlike the electric field due to a point charge which varies as $E \propto \dfrac{1}{{{r^2}}}$ . For a plane sheet having a definite thickness the net electric field at any point is given by $\vec E = \dfrac{\sigma }{{{ \in _0}}}\hat n$ . The SI unit of electric field is $N{C^{ - 1}}$.