Question

Three long straight wires in the XZ-plane, each carrying $I$, cross at the origin of coordinates, as shown in the figure below. Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} $ denote the unit vectors in the $x$, $y$ and $z$-directions respectively. The magnetic field as a function of $x$, with $y = 0$ and $z = 0$, is:

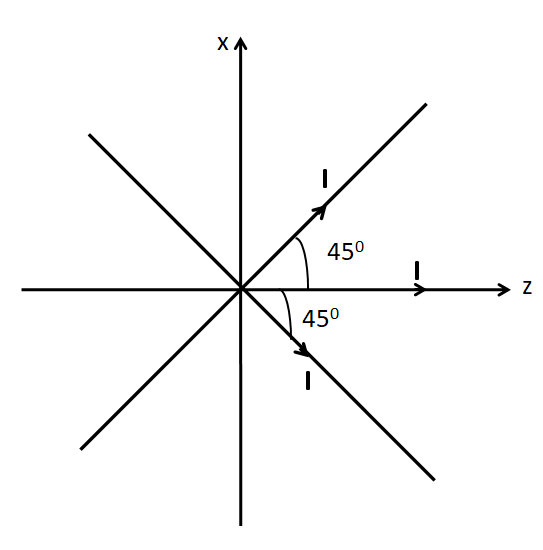
(A) $B = \dfrac{{3{\mu _0}I}}{{2\pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} $
(B) $B = \dfrac{{3{\mu _0}I}}{{2\pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
(C) $B = \dfrac{{{\mu _0}I}}{{2\pi x}}\left( {1 + 2\sqrt 2 } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
(D) $B = \dfrac{{{\mu _0}I}}{{2\pi x}}\left( {1 + 2\sqrt 2 } \right)\left( { - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} } \right)$

Answer 1

Hint To solve this question, we have to use the formula for the magnetic field due to an infinitely long carrying wire. And for getting the direction, we need to use the right hand thumb rule.
The formula which is used in solving this question is given by
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2\pi r}}$ , here $B$ is the magnetic field produced by an infinitely long wire carrying a current $I$ at a perpendicular distance of $r$ from it.

Complete step by step answer
Let us consider a point P on the x-axis at a distance of $x$ from the origin, as shown in the following figure.

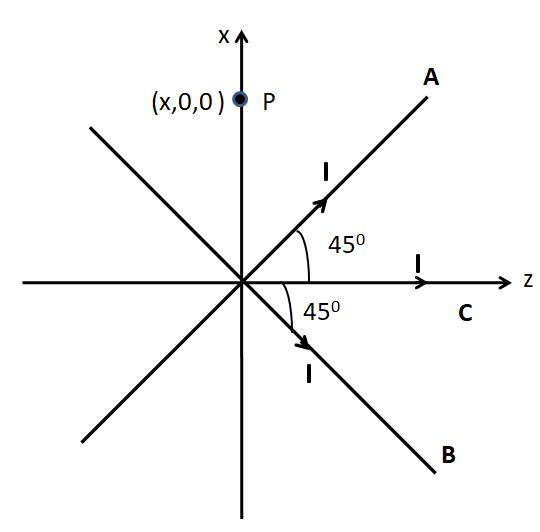
We know that the magnetic field due to an infinitely long wire is given by
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2\pi r}}$ (1)
So we need to calculate the perpendicular distance of the point P from each of the wires A, B and C.
For wire A:
Consider the following figure.

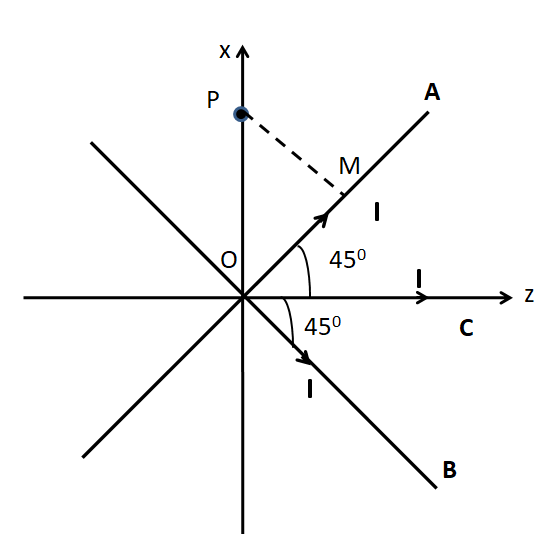
From the figure, we see that the perpendicular distance of the point P is
$\Rightarrow {r_1} = PM$
In the triangle $OPM$, we have
$\Rightarrow PM = OP\cos {45^ \circ }$
$\Rightarrow {r_1} = x\cos {45^ \circ }$
So we get
$\Rightarrow {r_1} = \dfrac{x}{{\sqrt 2 }}$ (2)
So from (1) the magnetic field due to wire A at the point P is
$\Rightarrow {B_A} = \dfrac{{{\mu _0}I}}{{2\pi {r_1}}}$
From (2)
$\Rightarrow {B_A} = \dfrac{{{\mu _0}I}}{{2\pi \dfrac{x}{{\sqrt 2 }}}}$
$\Rightarrow {B_A} = \dfrac{{{\mu _0}I}}{{\sqrt 2 \pi x}}$
By the right hand thumb rule, the direction of this field is along the positive y-axis. So in terms of the unit vector we have
$\Rightarrow {B_A} = \dfrac{{{\mu _0}I}}{{\sqrt 2 \pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
Similarly, the magnetic field due to the wire B at the point P
$\Rightarrow {B_B} = \dfrac{{{\mu _0}I}}{{\sqrt 2 \pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
Also, the magnetic field at P due to wire C is
$\Rightarrow {B_C} = \dfrac{{{\mu _0}I}}{{2\pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
So the net magnetic field at point P is
$\Rightarrow B = {B_A} + {B_B} + {B_C}$
From (3) (4) and (5)
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{\sqrt 2 \pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} + \dfrac{{{\mu _0}I}}{{\sqrt 2 \pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} + \dfrac{{{\mu _0}I}}{{2\pi x}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
On simplifying we get
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2\pi x}}\left( {1 + 2\sqrt 2 } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} $
Thus, this is the required magnetic field as a function of $x$.
Hence, the correct answer is option (C).

Note
The given set of axes is not the standard set of coordinate axes. So, for getting the direction of the positive y-axis, we use the right hand thumb rule. We should not assume the direction by ourselves.